
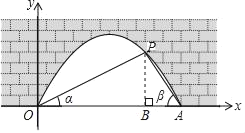
【题目】如图是抛物线形拱桥,P处有一照明灯,水面OA宽4m,从O、A两处双测P处,仰角分别为α、β,且tanα=![]() ,tanβ=
,tanβ=![]() ,以O为原点,OA所在直线为x轴建立直角坐标系. P点坐标为_____;若水面上升1m,水面宽为_____m.
,以O为原点,OA所在直线为x轴建立直角坐标系. P点坐标为_____;若水面上升1m,水面宽为_____m.
【答案】![]() ;
; ![]()
【解析】
(1)过点P作PH⊥OA于H,通过解Rt△OHP、Rt△AHP求得点P的横纵坐标;
(2)若水面上升1m后到达BC位置,如图,运用待定系数法可求出抛物线的解析式,然后求出y=1时x的值,就可解决问题.
解:(1)过点P作PH⊥OA于H,如图.
设PH=3x,
在Rt△OHP中,
∵tanα=![]() ,
,
∴OH=6x.
在Rt△AHP中,
∵tanβ=![]() ,
,
∴AH=2x,
∴OA=OH+AH=8x=4,
∴x=![]() ,
,
∴OH=3,PH=![]() ,
,
∴点P的坐标为(3,![]() );
);
故答案是:(3,![]() );
);
(2)若水面上升1m后到达BC位置,如图,

过点O(0,0),A(4,0)的抛物线的解析式可设为y=ax(x﹣4),
∵P(3,![]() )在抛物线y=ax(x﹣4)上,
)在抛物线y=ax(x﹣4)上,
∴3a(3﹣4)=![]() ,
,
解得a=﹣![]() ,
,
∴抛物线的解析式为y=﹣![]() x(x﹣4).
x(x﹣4).
当y=1时,﹣![]() x(x﹣4)=1,
x(x﹣4)=1,
解得x1=2+![]() ,x2=2﹣
,x2=2﹣![]() ,
,
∴BC=(2+![]() )﹣(2﹣
)﹣(2﹣![]() )=2
)=2![]() .
.
故答案是:2![]() .
.


科目:初中数学 来源: 题型:
【题目】家访是学校与家庭沟通的有效渠道,是形成教育合力的关键,是转化后进生的催化剂.某市教育局组织全市中小学教师开展家访活动活动过程中,教育局随机抽取了部分教师调查其近两周家访次数,将采集到的数据按家访次数分成五类,并分别绘制了下面的两幅不完整的统计图.
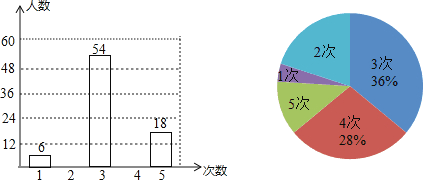
请根据以上信息,解答下列问题:
(1)请把条形统计图补充完整;
(2)所抽取的教师中,近两周家访次数的众数是 次,平均每位教师家访 次;
(3)若该市有12000名教师,请估计近两周家访不少于3次的教师有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的序号____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】扶贫工作小组对果农进行精准扶贫,帮助果农将一种有机生态水果拓宽了市场.与去年相比,今年这种水果的产量增加了1000千克,每千克的平均批发价比去年降低了1元,批发销售总额比去年增加了![]() .
.
(1)已知去年这种水果批发销售总额为10万元,求这种水果今年每千克的平均批发价是多少元?
(2)某水果店从果农处直接批发,专营这种水果.调查发现,若每千克的平均销售价为41元,则每天可售出300千克;若每千克的平均销售价每降低3元,每天可多卖出180千克,设水果店一天的利润为![]() 元,当每千克的平均销售价为多少元时,该水果店一天的利润最大,最大利润是多少?(利润计算时,其它费用忽略不计.)
元,当每千克的平均销售价为多少元时,该水果店一天的利润最大,最大利润是多少?(利润计算时,其它费用忽略不计.)
查看答案和解析>>
科目:初中数学 来源: 题型:
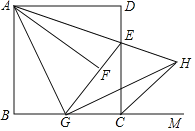
【题目】如图,在正方形![]() 中,
中,![]() 是
是![]() 边上一点,(与
边上一点,(与![]() 、
、![]() 不重合),连接
不重合),连接![]() ,将
,将![]() 沿
沿![]() 所在的直线折叠得到
所在的直线折叠得到![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,作
,作![]() ,与
,与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() .显然
.显然![]() 是
是![]() 的平分线,
的平分线,![]() 是
是![]() 的平分线.仔细观察,请逐一找出图中其他的角平分线(仅限于小于
的平分线.仔细观察,请逐一找出图中其他的角平分线(仅限于小于![]() 的角平分线),并说明理由.
的角平分线),并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() .
.

(1)如图①,点![]() 在斜边
在斜边![]() 上,以点
上,以点![]() 为圆心,
为圆心,![]() 长为半径的圆交
长为半径的圆交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,与边
,与边![]() 相切于点
相切于点![]() .求证:
.求证:![]() ;
;
(2)在图②中作![]() ,使它满足以下条件:
,使它满足以下条件:
①圆心在边![]() 上;②经过点
上;②经过点![]() ;③与边
;③与边![]() 相切.
相切.
(尺规作图,只保留作图痕迹,不要求写出作法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顶点为![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
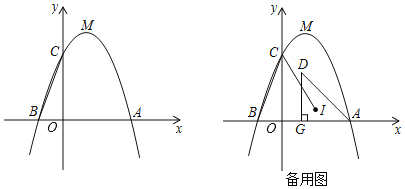
(1)求这条抛物线对应的函数表达式;
(2)问在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 为直角三角形?若存在,求出点
为直角三角形?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(3)若在第一象限的抛物线下方有一动点![]() ,满足
,满足![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() ,设
,设![]() 的内心为
的内心为![]() ,试求
,试求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生的阅读能力,我市某校开展了“读好书,助成长”的活动,并计划购置一批图书,购书前,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,请根据统计图回答下列问题:
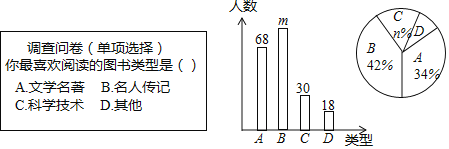
(1)本次调查共抽取了 名学生,两幅统计图中的m= ,n= .
(2)已知该校共有3600名学生,请你估计该校喜欢阅读“A”类图书的学生约有多少人?
(3)学校将举办读书知识竞赛,九年级1班要在本班3名优胜者(2男1女)中随机选送2人参赛,请用列表或画树状图的方法求被选送的两名参赛者为一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在扇形OAB中,点C是弧AB上任意一点(不与点A,B重合),CD∥OA交OB于点D,点I是△OCD的内心,连结OI,BI.若∠AOB=β,则∠OIB等于( )

A. 180°![]() βB. 180°-βC. 90°+
βB. 180°-βC. 90°+ ![]() βD. 90°+β
βD. 90°+β
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com