
【题目】根据有理数乘法(除法)法则可知:①若![]() (或
(或![]() ),则
),则![]() 或
或![]() ;②若
;②若![]() (或
(或![]() ),则
),则![]() 或
或![]() .
.
根据上述知识,求不等式![]() 的解集:
的解集:
解:原不等式可化为:(1)![]() 或(2)
或(2)![]() .
.
由(1)得,![]() ,由(2)得,
,由(2)得,![]() ,
,
∴原不等式的解集为:![]() 或
或![]()
请你运用所学知识,结合上述材料解答下列问题:
(1)不等式![]() 的解集为 .
的解集为 .
(2)求不等式![]() 的解集(要求写出解答过程)
的解集(要求写出解答过程)
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
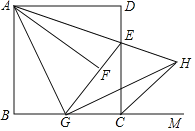
【题目】如图,在正方形![]() 中,
中,![]() 是
是![]() 边上一点,(与
边上一点,(与![]() 、
、![]() 不重合),连接
不重合),连接![]() ,将
,将![]() 沿
沿![]() 所在的直线折叠得到
所在的直线折叠得到![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,作
,作![]() ,与
,与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() .显然
.显然![]() 是
是![]() 的平分线,
的平分线,![]() 是
是![]() 的平分线.仔细观察,请逐一找出图中其他的角平分线(仅限于小于
的平分线.仔细观察,请逐一找出图中其他的角平分线(仅限于小于![]() 的角平分线),并说明理由.
的角平分线),并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
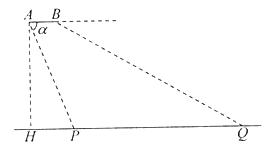
【题目】如图,从一架水平飞行的无人机![]() 的尾端点
的尾端点![]() 测得正前方的桥的左端点
测得正前方的桥的左端点![]() 俯角为
俯角为![]() ,且
,且![]() ,无人机的飞行高度
,无人机的飞行高度![]() 米,桥的长度
米,桥的长度![]() 为1255米.
为1255米.
(1)求点![]() 到桥左端点
到桥左端点![]() 的距离;
的距离;
(2)若从无人机前端点![]() 测得正前方的桥的右端点
测得正前方的桥的右端点![]() 的俯角为
的俯角为![]() ,求这架无人机的长度
,求这架无人机的长度![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.①抛物线
(m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.①抛物线![]() 与直线
与直线![]() 有且只有一个交点;②若点
有且只有一个交点;②若点![]() 、点
、点![]() 、点
、点![]() 在该函数图象上,则
在该函数图象上,则![]() ;③将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为
;③将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为![]() ;④点A关于直线
;④点A关于直线![]() 的对称点为C,点D、E分别在x轴和y轴上,当
的对称点为C,点D、E分别在x轴和y轴上,当![]() 时,四边形BCDE周长的最小值为
时,四边形BCDE周长的最小值为![]() .其中正确判断的序号是__
.其中正确判断的序号是__

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在扇形OAB中,点C是弧AB上任意一点(不与点A,B重合),CD∥OA交OB于点D,点I是△OCD的内心,连结OI,BI.若∠AOB=β,则∠OIB等于( )

A. 180°![]() βB. 180°-βC. 90°+
βB. 180°-βC. 90°+ ![]() βD. 90°+β
βD. 90°+β
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学拓展课上,老师给出如下定义:如果三角形有一边上的中线长恰好等于该边长的1.5倍,那么称这个三角形为“趣味三角形”.
理解:
(1)如图1,在△ABC中,AB=AC=![]() ,BC=2,试判断△ABC是否为“趣味三角形”,并说明理由.
,BC=2,试判断△ABC是否为“趣味三角形”,并说明理由.
(2)如图2,已知△ABC是“趣味三角形”,AD,BE,CF分别是BC,AC,AB边上的中线,且AD=![]() BC,试探究BE和CF之间的位置关系.
BC,试探究BE和CF之间的位置关系.
(3)如图3,直线l1∥l2 , l1与l2之间的距离为2,点B,C在直线l1上,点A在直线l2上,AD,BE,CF分别是△ABC的边BC,AC,AB上的中线.若△ABC是“趣味三角形”,BC=2![]() .求BE2+CF2的值.
.求BE2+CF2的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
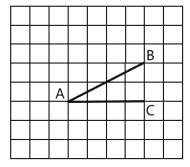
【题目】如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上。
(I)AB的长度等于
(II)请你在图中找到一个点P,使得AB是∠PAC的角平分线请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
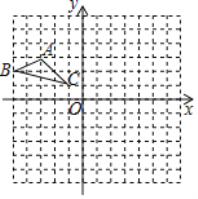
【题目】△ABC在边长为l的正方形网格中如图所示.
①以点C为位似中心,作出△ABC的位似图形△A1B1C,使其位似比为1:2.且△A1B1C位于点C的异侧,并表示出A1的坐标.
②作出△ABC绕点C顺时针旋转90°后的图形△A2B2C.
③在②的条件下求出点B经过的路径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com