
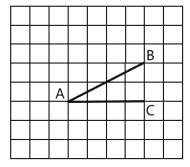
【题目】如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上。
(I)AB的长度等于
(II)请你在图中找到一个点P,使得AB是∠PAC的角平分线请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明)
科目:初中数学 来源: 题型:
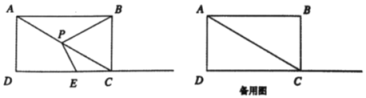
【题目】如图,四边形ABCD是矩形,点P是对角线AC上一动点(不与A、C 重合),连接PB,过点P作PE⊥PB,交射线DC于点E,已知AD=3,sin∠BAC=![]() .设AP的长为x.
.设AP的长为x.
(1)AB等于多少;当x=1时,![]() 等于多少;
等于多少;
(2)①试探究: ![]() 否是定值?若是,请求出这个值;若不是,请说明理由;
否是定值?若是,请求出这个值;若不是,请说明理由;
②连接BE,设△PBE的面积为S,求S的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
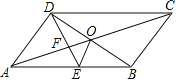
【题目】如图,ABCD的对角线AC、BD交于点O,DE平分∠ADC交AB于点E,∠BCD=60°,AD=![]() AB,连接OE.下列结论:①SABCD=ADBD;②DB平分∠CDE;③AO=DE;④S△ADE=5S△OFE,其中正确的个数有( )
AB,连接OE.下列结论:①SABCD=ADBD;②DB平分∠CDE;③AO=DE;④S△ADE=5S△OFE,其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
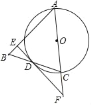
【题目】如图,在△ABC中,AB=AC,以AC为直经作⊙O交BC与D点,过点D作⊙O的切线EF,交AB于点E,交AC的延长线于点F.
(1)求证:FE⊥AB.
(2)当AE=6,AF=10时,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌笔记本电脑的售价是5000元/台。最近,该商家对此型号笔记本电脑举行促销活动,有两种优惠方案。方案一:每台按售价的九折销售,方案二:若购买不超过5台,每台按售价销售;若超过5台,超过的部分每台按售价的八折销售。设公司一次性购买此型号笔记本电脑x合、
(I)根据题意,填写下表:

(II)设选择方案一的费用为y1元,选择方案二的费用为为y2元,分别写出y1,y2关于x的函数关系式;
(III)当x>15时,该公司采用哪种方案购买更合算?并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校2400名学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.将调查得到的结果绘制成如图所示的频数分布直方图和扇形统计图(均不完整).
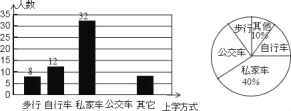
(1)问:在这次调查中,一共抽取了多少名学生?
(2)补全频数分布直方图;
(3)估计全校所有学生中有多少人乘坐公交车上学;
(4)为了鼓励“低碳生活”,学校为随机抽到的步行或骑自行车上学的学生设计了一个摸奖游戏,具体规则如下:一个不透明的袋子中装着标有数字1、2、3、4的四个完全相同的小球,随机地从四个小球中摸出一球然后放回,再随机地摸出一球,若第二次摸出的小球标有的数字比第一次摸出的小球标有的数字大,则有小礼物赠送,问获得小礼物的概率是多少(用树状图或列表说明)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的袋子中装有4个相同的小球,它们除颜色外无其它差别,把它们分别标号:1、2、3、4,
(1)随机摸出一个小球后,放回并摇匀,再随机摸出一个,用列表或画树状图的方法求出“两次取的球标号相同”的概率
(2)随机摸出两个小球,直接写出“两次取出的球标号和等于4”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCO的顶点B、C在第二象限,点A(﹣3,0),反比例函数y=![]() (k<0)图象经过点C和AB边的中点D,若∠B=α,则k的值为( )
(k<0)图象经过点C和AB边的中点D,若∠B=α,则k的值为( )

A. ﹣4tanαB. ﹣2sinαC. ﹣4cosαD. ﹣2tan
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com