
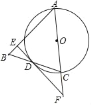
【题目】如图,在△ABC中,AB=AC,以AC为直经作⊙O交BC与D点,过点D作⊙O的切线EF,交AB于点E,交AC的延长线于点F.
(1)求证:FE⊥AB.
(2)当AE=6,AF=10时,求BE的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)连接OD,由EF为⊙O的切线,利用切线的性质得到OD与EF垂直,利用同圆的半径相等和等边对等角得到OD∥AB,由与平行线中的一条直线垂直,与另一条也垂直,即可得证;
(2)如图2,连接OD,过O作OG⊥AB于G,先根据勾股定理求EF=8,根据三角函数tan∠F=![]() =
=![]() =
=![]() =
= ![]() ,设OD=3x,DF=4x,则OF=5x,表示AG=
,设OD=3x,DF=4x,则OF=5x,表示AG=![]() ,根据AE=6,列方程3x+
,根据AE=6,列方程3x+![]() =6,可得x的值,计算BE的长.
=6,可得x的值,计算BE的长.
证明:(1)如图1,连接OD,
∵OC=OD,
∴∠ODC=∠OCD,
又∵AB=AC,
∴∠OCD=∠B,
∴∠ODC=∠B,
∴OD∥AB,
∵ED是⊙O的切线,OD是⊙O的半径,
∴OD⊥EF,
∴AB⊥EF;
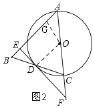
(2)如图2,连接OD,过O作OG⊥AB于G,
Rt△AEF中,∵AE=6,AF=10,
∴EF=8,
tan∠F=![]() =
=![]() =
=![]() =
= ![]() ,
,
设OD=3x,DF=4x,则OF=5x,
∴OA=OC=3x,FC=2x,
∵OG∥EF,
∴∠AOG=∠F,
∴sin∠AOG=sin∠F=![]() =
=![]() ,
,
∴![]() =
=![]() =
= ![]() ,
,
∴AG=![]() ,
,
∵四边形EDOG为矩形,
∴EG=OD=3x,
∵AE=6,
∴3x+![]() =6,
=6,
x=![]() ,
,
∴BE=AB﹣AE=AC﹣AE=6x﹣6=6×![]() ﹣6=
﹣6=![]() .
.


科目:初中数学 来源: 题型:
【题目】暑假是旅游旺季,为吸引游客,某旅游公司推出两条“精品路线”——“亲子游”和“夏令营”。(1)7月份,“亲子游”和“夏令营”活动的价格分别为8000元/人和12000元/人。其中,参加“夏令营”活动的游客人数为“亲子游”活动游客人数的2倍少300人,且“夏令营”线路的旅游总收入不低于“亲子游”线路旅游总收入的一半,
问:(1)参加“亲子游”线路的旅游人数至少有多少人?
(2)到了8月份,该旅游公司实行降价促销活动,“亲子游”和“夏令营”线路的价格分别下降![]() 和
和![]() (
(![]() <20),旅游人数在7月份对应最小值的基础上分别上升
<20),旅游人数在7月份对应最小值的基础上分别上升![]() 和
和![]() ,当月旅游总收入达到256.32万元,求
,当月旅游总收入达到256.32万元,求![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承中华优秀传统文化,某校组织了一次八年级350名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩(成绩![]() 取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 2 | 0.04 |
60≤x<70 | 6 | 0.12 |
70≤x<80 | 9 |
|
80≤x<90 | 0.36 | |
90≤x≤100 | 15 | 0.30 |

请根据所给信息,解答下列问题:
(1)a等于多少,b等于多少;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在哪个分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该年级参加这次比赛的350名学生中成绩“优”等的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=4,将对角线AC绕对角线交点O旋转,分别交边AD、BC于点E、F,点P是边DC上的一个动点,且保持DP=AE,连接PE、PF,设AE=x(0<x<3).
(1)填空:PC= ,FC= ;(用含x的代数式表示)
(2)求△PEF面积的最小值;
(3)在运动过程中,PE⊥PF是否成立?若成立,求出x的值;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点O从边长为6的等边△ABC的顶点A出发,沿着ACBA的路线匀速运动一周,速度为1个单位长度每秒,以O为圆心、![]()
![]() 为半径的圆在运动过程中与△ABC的边第二次相切时是点O出发后第______秒.
为半径的圆在运动过程中与△ABC的边第二次相切时是点O出发后第______秒.

查看答案和解析>>
科目:初中数学 来源: 题型:
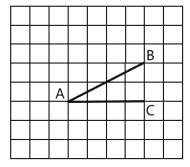
【题目】如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上。
(I)AB的长度等于
(II)请你在图中找到一个点P,使得AB是∠PAC的角平分线请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已如抛物线y=-x2+3x+m,其中m为常数
(I)当抛物线经过点(3,5)时,求该抛物线的解析式。
(II)当抛物线与直线y=x+3m只有一个交点时,求该抛物线的解析式。
(III)当0≤x≤4时,试通过m的取值范围讨论抛物线与直线y=x+2的公共点的个数的情况
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对非负实数x“四舍五入”到个位的值记为[x].即当n为非负整数时,若n﹣![]() ≤x<n+
≤x<n+![]() ,则[x]=n.如:[2.9]=3;[2.4]=2;……根据以上材料,解决下列问题:
,则[x]=n.如:[2.9]=3;[2.4]=2;……根据以上材料,解决下列问题:
(1)填空[1.8]= ,[![]() ]= ;
]= ;
(2)若[2x+1]=4,则x的取值范围是 ;
(3)求满足[x]=![]() x﹣1的所有非负实数x的值.
x﹣1的所有非负实数x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com