
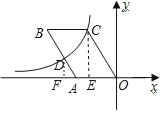
【题目】如图,ABCO的顶点B、C在第二象限,点A(﹣3,0),反比例函数y=![]() (k<0)图象经过点C和AB边的中点D,若∠B=α,则k的值为( )
(k<0)图象经过点C和AB边的中点D,若∠B=α,则k的值为( )

A. ﹣4tanαB. ﹣2sinαC. ﹣4cosαD. ﹣2tan
【答案】A
【解析】
过点C作CE⊥OA于E,过点D作DF⊥x轴于F,根据平行四边形的对边相等可得OC=AB,然后求出OC=2AD,再求出OE=2AF,设AF=a,表示出点C、D的坐标,然后根据CE、DF的关系列方程求出a的值,再求出OE、CE,然后利用∠COA的正切值列式整理即可得解.
如图,过点C作CE⊥OA于E,过点D作DF⊥x轴于F,
在OABC中,OC=AB,
∵D为边AB的中点,
∴OC=AB=2AD,CE=2DF,
∴OE=2AF,
设AF=a,∵点C、D都在反比例函数上,
∴点C(﹣2a,﹣![]() ),
),
∵A(3,0),
∴D(﹣a﹣3,![]() ),
),
∴-![]() =2×
=2×![]() ,
,
解得a=1,
∴OE=2,CE=﹣![]() ,
,
∵∠COA=∠α,
∴tan∠COA=tan∠α=![]() ,
,
即tanα=﹣![]() ,
,
k=﹣4tanα,
故选A.


科目:初中数学 来源: 题型:
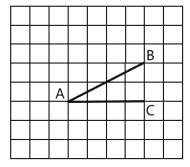
【题目】如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上。
(I)AB的长度等于
(II)请你在图中找到一个点P,使得AB是∠PAC的角平分线请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AC的表达式为y=![]() x+8,点P从点A开始沿AO向点O以1个单位/s的速度移动,点Q从点O开始沿OC向点C以2个单位/s的速度移动.如果P,Q两点分别从点A,O同时出发,经过几秒能使△PQO的面积为8个平方单位?
x+8,点P从点A开始沿AO向点O以1个单位/s的速度移动,点Q从点O开始沿OC向点C以2个单位/s的速度移动.如果P,Q两点分别从点A,O同时出发,经过几秒能使△PQO的面积为8个平方单位?

查看答案和解析>>
科目:初中数学 来源: 题型:
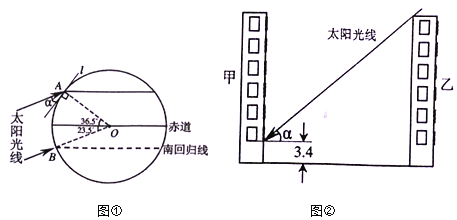
【题目】图①,②是晓东同学在进行“居民楼高度、楼间距对住户采光影响问题”的研究时画的两个示意图.请你阅读相关文字,解答下面的问题.
(1)图①是太阳光线与地面所成角度的示意图.冬至日正午时刻,太阳光线直射在南回归线(南纬23.5)B地上.在地处北纬36.5的A地,太阳光线与地面水平线l所成的角为![]() ,试借助图①,求
,试借助图①,求![]() 的度数.
的度数.
(2)图②是乙楼高度、楼间距对甲楼采光影响的示意图.甲楼地处A地,其二层住户的南面窗户下沿距地面3.4米.现要在甲楼正南面建一幢高度为22.3米的乙楼,为不影响甲楼二层住户(一层为车库)的采光,两楼之间的距离至少应为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对非负实数x“四舍五入”到个位的值记为[x].即当n为非负整数时,若n﹣![]() ≤x<n+
≤x<n+![]() ,则[x]=n.如:[2.9]=3;[2.4]=2;……根据以上材料,解决下列问题:
,则[x]=n.如:[2.9]=3;[2.4]=2;……根据以上材料,解决下列问题:
(1)填空[1.8]= ,[![]() ]= ;
]= ;
(2)若[2x+1]=4,则x的取值范围是 ;
(3)求满足[x]=![]() x﹣1的所有非负实数x的值.
x﹣1的所有非负实数x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
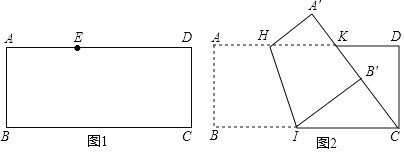
【题目】有一张矩形纸片ABCD,![]() ,
,![]() .
.
![]() 如图1,点E在这张矩形纸片的边AD上,将纸片折叠,使AB落在CE所在直线上,折痕设为
如图1,点E在这张矩形纸片的边AD上,将纸片折叠,使AB落在CE所在直线上,折痕设为![]() 点M,N分别在边AD,BC上
点M,N分别在边AD,BC上![]() ,利用直尺和圆规画出折痕
,利用直尺和圆规画出折痕![]() 不写作法,保留作图痕迹
不写作法,保留作图痕迹![]() ;
;
![]() 如图2,点K在这张矩形纸片的边AD上,
如图2,点K在这张矩形纸片的边AD上,![]() ,将纸片折叠,使AB落在CK所在直线上,折痕为HI,点A,B分别落在点
,将纸片折叠,使AB落在CK所在直线上,折痕为HI,点A,B分别落在点![]() ,
,![]() 处,小明认为
处,小明认为![]() 所在直线恰好经过点D,他的判断是否正确,请说明理由.
所在直线恰好经过点D,他的判断是否正确,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:

(1)接受问卷调查的学生共有_______人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_______°;
(2)请补全条形统计图;
(3)若该中学共有学生1800人,请根据上述调查结果,估计该中学学生中对校园安全知识 达到“了解”和“基本了解”程度的总人数;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,A是反比例函数y=![]() (x>0)图象上一点,B是y轴正半轴上一点,以OA,AB为邻边作ABCO.若点C及BC中点D都在反比例函数y=
(x>0)图象上一点,B是y轴正半轴上一点,以OA,AB为邻边作ABCO.若点C及BC中点D都在反比例函数y=![]() (k<0,x<0)图象上,则k的值为( )
(k<0,x<0)图象上,则k的值为( )
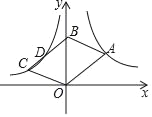
A. ﹣3B. ﹣4C. ﹣6D. ﹣8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“宜居襄阳”是我们的共同愿景,空气质量备受人们关注.我市某空气质量监测站点检测了该区域每天的空气质量情况,统计了2013年1月份至4月份若干天的空气质量情况,并绘制了如下两幅不完整的统计图.
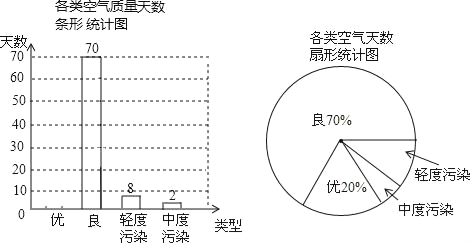
请根据图中信息,解答下列问题:
(1)统计图共统计了 天的空气质量情况;
(2)请将条形统计图补充完整;空气质量为“优”所在扇形的圆心角度数是 ;
(3)从小源所在环保兴趣小组4名同学(2名男同学,2名女同学)中,随机选取两名同学去该空气质量监测站点参观,则恰好选到一名男同学和一名女同学的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com