
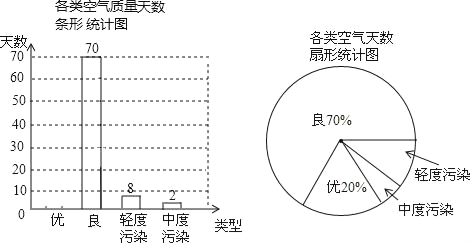
【题目】“宜居襄阳”是我们的共同愿景,空气质量备受人们关注.我市某空气质量监测站点检测了该区域每天的空气质量情况,统计了2013年1月份至4月份若干天的空气质量情况,并绘制了如下两幅不完整的统计图.
请根据图中信息,解答下列问题:
(1)统计图共统计了 天的空气质量情况;
(2)请将条形统计图补充完整;空气质量为“优”所在扇形的圆心角度数是 ;
(3)从小源所在环保兴趣小组4名同学(2名男同学,2名女同学)中,随机选取两名同学去该空气质量监测站点参观,则恰好选到一名男同学和一名女同学的概率是 .
科目:初中数学 来源: 题型:
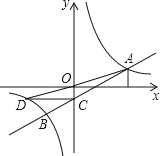
【题目】如图,ABCO的顶点B、C在第二象限,点A(﹣3,0),反比例函数y=![]() (k<0)图象经过点C和AB边的中点D,若∠B=α,则k的值为( )
(k<0)图象经过点C和AB边的中点D,若∠B=α,则k的值为( )

A. ﹣4tanαB. ﹣2sinαC. ﹣4cosαD. ﹣2tan
查看答案和解析>>
科目:初中数学 来源: 题型:
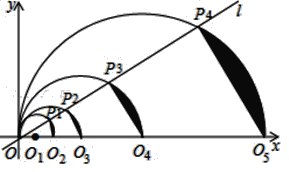
【题目】如图,在平面直角坐标系中,直线l的函数表达式为y=![]() x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画半圆,交直线l于点P1,交x轴正半轴于点O2,由弦P1O2和
x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画半圆,交直线l于点P1,交x轴正半轴于点O2,由弦P1O2和![]() 围成的弓形面积记为S1,以O2为圆心,O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3,由弦P2O3和围
围成的弓形面积记为S1,以O2为圆心,O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3,由弦P2O3和围![]() 成的弓形面积记为S2,以O3为圆心,O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4,由弦P3O4和
成的弓形面积记为S2,以O3为圆心,O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4,由弦P3O4和![]() 围成的弓形面积记为S3;…按此做法进行下去,其中S2018的面积为__________.
围成的弓形面积记为S3;…按此做法进行下去,其中S2018的面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,等边△ABC内接于⊙O,点P是⌒AB上的任意一点,连结PA,PB,PC.点D是PC上一点,连结DB.
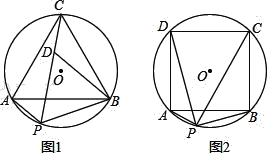
(1) 若PD=PB,求∠PBD的度数;
(2)在(1)的条件下,小丽探究![]() 的值,她认为只要弄清PA+PB与PC的关系即可,她的思路可以用以下框图表示:
的值,她认为只要弄清PA+PB与PC的关系即可,她的思路可以用以下框图表示:

根据小丽的思路,请你完整地书写本题的探究过程,并求出![]() 的值.
的值.
(3)如图2,把条件“等边△ABC”改为“正方形ABCD”,其余条件不变,判断![]() 是定值吗?若是,请求出这个值;若不是,请说明理由.
是定值吗?若是,请求出这个值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
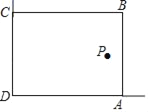
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用32m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为252m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是17m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
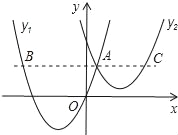
【题目】如图,抛物线y1=a(x+2)2﹣3与y2=![]() (x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结沦:①无论x取何值,y2的值总是正数;②2a=1;③当x=0时,y2﹣y1=4;④2AB=3AC;其中正确结论是( )
(x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结沦:①无论x取何值,y2的值总是正数;②2a=1;③当x=0时,y2﹣y1=4;④2AB=3AC;其中正确结论是( )
A. ①②B. ②③C. ③④D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知开口向上的抛物线y=ax2+bx+c与x轴交于A(﹣3,0)、B(1,0)两点,与y轴交于C点,∠ACB不小于90°.
(1)求点C的坐标(用含a的代数式表示);
(2)求系数a的取值范围;
(3)设抛物线的顶点为D,求△BCD中CD边上的高h的最大值.
(4)设E(-![]() ,0),当∠ACB=90°,在线段AC上是否存在点F,使得直线EF将△ABC的面积平分?若存在,求出点F的坐标;若不存在,说明理由.
,0),当∠ACB=90°,在线段AC上是否存在点F,使得直线EF将△ABC的面积平分?若存在,求出点F的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知正方形的边长为a,将此正方形按照下面的方法进行剪拼:第一次,先沿正方形的对边中点连线剪开,然后对接为一个长方形,则此长方形的周长为___;第二次,再沿长方形的对边(长方形的宽)中点连线剪开,对接为新的长方形,如此继续下去,第n次得到的长方形的周长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b与反比例函数y=![]() 的图象交于A、B两点,点A坐标为(m,2),点B坐标为(﹣4,n),OA与x轴正半轴夹角的正切值为
的图象交于A、B两点,点A坐标为(m,2),点B坐标为(﹣4,n),OA与x轴正半轴夹角的正切值为![]() ,直线AB交y轴于点C,过C作y轴的垂线,交反比例函数图象于点D,连接OD、BD.
,直线AB交y轴于点C,过C作y轴的垂线,交反比例函数图象于点D,连接OD、BD.
(1)求一次函数与反比例函数的解析式;
(2)求四边形OCBD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com