
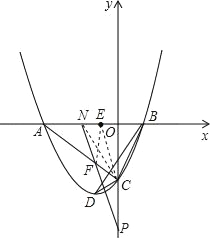
����Ŀ����֪�������ϵ�������y��ax2+bx+c��x�ύ��A����3��0����B��1��0�����㣬��y�ύ��C�㣬��ACB��С��90����
��1�����C�����꣨�ú�a�Ĵ���ʽ��ʾ����
��2����ϵ��a��ȡֵ��Χ��
��3���������ߵĶ���ΪD������BCD��CD���ϵĸ�h�����ֵ��
��4����E(-![]() ��0)������ACB��90�������߶�AC���Ƿ���ڵ�F��ʹ��ֱ��EF����ABC�����ƽ�֣������ڣ������F�����ꣻ�������ڣ�˵�����ɣ�
��0)������ACB��90�������߶�AC���Ƿ���ڵ�F��ʹ��ֱ��EF����ABC�����ƽ�֣������ڣ������F�����ꣻ�������ڣ�˵�����ɣ�

���𰸡���1����C������Ϊ��0����3a������2��0��a��![]() ����3��1����4������ACB��90�������߶�AC�ϴ��ڵ�F��ʹ��ֱ��EF����ABC�����ƽ�֣���F�������ǣ���
����3��1����4������ACB��90�������߶�AC�ϴ��ڵ�F��ʹ��ֱ��EF����ABC�����ƽ�֣���F�������ǣ���![]() ����
����![]() ����
����
��������
��1���������� y��ax2+bx+c����A����3��0����B��1��0�����ó�c��a�Ĺ�ϵ�����ɵó�C�����ꣻ
��2��������֪�ó���AOC�ס�COB���������OC�ij��ȣ����ɵó�a��ȡֵ��Χ��
��3����DG��y���ڵ�G���ӳ�DC��x���ڵ�H���ó������ߵĶԳ���Ϊx����1�����������DCG�ס�HCO���ó�OH��3����B��BM��DH������ΪM����BM��h������h��HB sin��OHC���0������OHC��30�����õ�0��sin��OHC��![]() ����������𰸣�
����������𰸣�
��4������CE������N��NP��CD��y����P������EF�����������ε������ʽ���S��CAEF��S�ı���EFCB������NP��CE�����P��0��-2![]() �������N��P�����һ�κ�����y��kx+b������N��P����ߵõ������飬���ֱ��NP�Ľ���ʽ��ͬ�����A��C�����ֱ�ߵĽ���ʽ����ɷ�����������ɣ�
�������N��P�����һ�κ�����y��kx+b������N��P����ߵõ������飬���ֱ��NP�Ľ���ʽ��ͬ�����A��C�����ֱ�ߵĽ���ʽ����ɷ�����������ɣ�
��1���������� y��ax2+bx+c����A����3��0����B��1��0����
��![]() ��ȥb���� c����3a��
��ȥb���� c����3a��
���C��������0����3a����
�𣺵�C������Ϊ��0����3a����
��2������ACB��90��ʱ��
��AOC����BOC��90������OBC+��BCO��90������ACO+��BCO��90����
���ACO����OBC��
���AOC�ס�COB��
��![]() ��
��
�� OC2��AOOB��
��AO��3��OB��1��
��OC��![]() ��
��
�ߡ�ACB��С��90����
��OC��![]() ������c��
������c��![]() ��
��
�ɣ�1���� 3a��![]() ��
��
��a��![]() ��
��
�֡�a��0��
��a��ȡֵ��ΧΪ0��a��![]() ��
��
��ϵ��a��ȡֵ��Χ��0��a��![]() ��
��
��3����DG��y���ڵ�G���ӳ�DC��x���ڵ�H����ͼ��
�������� y��ax2+bx+c��x����A����3��0����B��1��0����
�������ߵĶԳ���Ϊx����1��
����![]() ����1������b��2a��
����1������b��2a��
���ɣ�1����c����3a��
�������߷���Ϊ y��ax2+2ax��3a��D������Ϊ����1����4a����
���� CO��3a��GC��a��DG��1��
��DG��OH��
���DCG�ס�HCO��
��![]() ����
����![]() ���� OH��3������ֱ��DC������H��3��0����
���� OH��3������ֱ��DC������H��3��0����
��B��BM��DH������ΪM����BM��h��
��h��HB sin��OHC��2 sin��OHC��
��0��CO��![]() ��
��
��0������OHC��30����0��sin��OHC��![]() ��
��
��0��h��1����h�����ֵΪ1��
����BCD��CD���ϵĸ�h�����ֵ��1��
��4���ɣ�1������2����֪������ACB��90��ʱ��a=![]() ��CO=
��CO=![]() ��
��
��AB���е�ΪN������CN����N����1��0����CN����ABC�����ƽ�֣�
����CE������N��NP��CE��y����P����Ȼ��P��OC���ӳ����ϣ��Ӷ�NP����AC�ཻ�����佻��ΪF������EF��
��ΪNP��CE������S��CEF��S��CEN��
����֪�ɵ�NO��1��EO=![]() ����NP��CE��
����NP��CE��
��PO=2CO=2![]() ����P��0��-2
����P��0��-2![]() ����
����
���N��P�����һ�κ�����y��kx+b����![]() ��
��
��ã�k=b=-2![]() ��
��
��y=-2![]() (x+1)����
(x+1)����
ͬ���ɵù�A��C�����һ�κ���Ϊx+![]() y+3=0����
y+3=0����
���ɢ٢���ɵķ������x=-![]() ��y=-
��y=-![]() ��
��
�����߶�AC�ϴ��ڵ�F(-![]() ,-
,-![]() )����Ҫ��
)����Ҫ��
�𣺵���ACB��90�������߶�AC�ϴ��ڵ�F��ʹ��ֱ��EF����ABC�����ƽ�֣���F��������(-![]() ,-
,-![]() )��
)��


 �߲������Ӧ��һ��ͨϵ�д�
�߲������Ӧ��һ��ͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
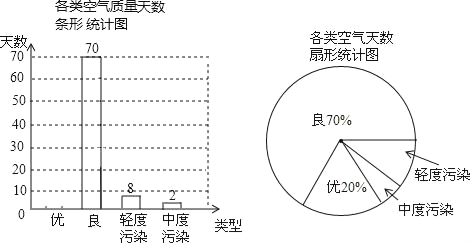
����Ŀ����У��ȫ���ܵ�ȫ���Ĺ㷺��ע������ij��ѧ�Բ���ѧ����У��ȫ֪ʶ���˽�̶ȣ����������������ķ�ʽ���������ռ�������Ϣ����ͳ�ƣ����������������в�������ͳ��ͼ���������ͳ��ͼ�����ṩ����Ϣ����������⣺

(1)�����ʾ������ѧ������_______�ˣ�����ͳ��ͼ���������˽�����������Ӧ���ε�Բ�Ľ�Ϊ_______�㣻
(2)�벹ȫ����ͳ��ͼ��
(3)������ѧ����ѧ��1800�ˣ���������������������Ƹ���ѧѧ���ж�У��ȫ֪ʶ �ﵽ���˽������������˽����̶ȵ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬B��x���ϣ��ı���OACBΪƽ���ı��Σ���
��AOB=60�㣬����������![]() ��k��0���ڵ�һ�����ڹ���A������BC���ڵ�F����FΪBC���е㣬��S��AOF��12
��k��0���ڵ�һ�����ڹ���A������BC���ڵ�F����FΪBC���е㣬��S��AOF��12![]() ʱ��OA�ij�Ϊ____.
ʱ��OA�ij�Ϊ____.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����˾������������ǵĹ�ͬԸ�������������������ǹ�ע������ij�����������վ�����˸�����ÿ��Ŀ������������ͳ����2013��1�·���4�·�������Ŀ������������������������������������ͳ��ͼ��
�����ͼ����Ϣ������������⣺
��1��ͳ��ͼ��ͳ������ ����Ŀ������������
��2���뽫����ͳ��ͼ������������������Ϊ�������������ε�Բ�ĽǶ������� ����
��3����СԴ���ڻ�����ȤС��4��ͬѧ��2����ͬѧ��2��Ůͬѧ���У����ѡȡ����ͬѧȥ�ÿ����������վ��ιۣ���ǡ��ѡ��һ����ͬѧ��һ��Ůͬѧ�ĸ������� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
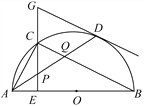
����Ŀ����ͼ���ڡ�O�У�AB��ֱ������D�ǡ�O��һ�㣬��C��![]() ���е㣬CE��AB�ڵ�E������D�����߽�EC���ӳ����ڵ�G������AD���ֱ�CE��CB�ڵ�P��Q������AC���������н��ۣ��١�BAD����ABC����GP��GD���۵�P�ǡ�ACQ�����ģ����н�����ȷ����________(ֻ����д���)��
���е㣬CE��AB�ڵ�E������D�����߽�EC���ӳ����ڵ�G������AD���ֱ�CE��CB�ڵ�P��Q������AC���������н��ۣ��١�BAD����ABC����GP��GD���۵�P�ǡ�ACQ�����ģ����н�����ȷ����________(ֻ����д���)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
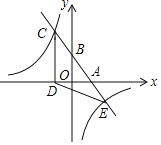
����Ŀ����ͼ��һ�κ���y=kx+b��k��bΪ������k��0����ͼ����x�ᡢy��ֱ���A��B���㣬���뷴��������y=![]() ��nΪ��������n��0����ͼ���ڵڶ������ڵ�C��CD��x�ᣬ����ΪD����OB=2OA=3OD=12��
��nΪ��������n��0����ͼ���ڵڶ������ڵ�C��CD��x�ᣬ����ΪD����OB=2OA=3OD=12��
��1����һ�κ����뷴���������Ľ���ʽ��
��2����������ͼ�����һ������ΪE�����CDE�������
��3��ֱ��д������ʽkx+b��![]() �Ľ⼯��
�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
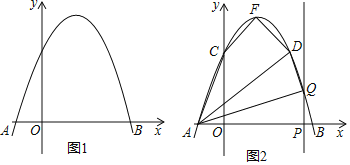
����Ŀ����ͼ1��������y=ax2+bx+3��x���ڵ�A����1��0���͵�B��3��0����
��1���������������Ӧ�ĺ�������ʽ��
��2����ͼ2������������y�ύ�ڵ�C������ΪF����D��2��3���ڸ��������ϣ�
�����ı���ACFD�������
�ڵ�P���߶�AB�ϵĶ��㣨��P�����A��B�غϣ�������P��PQ��x�ύ���������ڵ�Q������AQ��DQ������AQD��ֱ��������ʱ������������������ĵ�Q�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����![]() ������AC������C��ֱ��l��AB����P��ֱ��l�ϵ�һ�����㣬ֱ��PA���O������һ��D������CD����ֱ��PB��ֱ��AC���ڵ�E��
������AC������C��ֱ��l��AB����P��ֱ��l�ϵ�һ�����㣬ֱ��PA���O������һ��D������CD����ֱ��PB��ֱ��AC���ڵ�E��
��1�����BAC�Ķ�����
��2������D��AB�Ϸ�����CD��BPʱ����֤��PC=AC��
��3���ڵ�P���˶�������
�ٵ���A���߶�PB���д����ϻ��B���߶�PA���д�����ʱ������������������ġ�ACD�Ķ�����
�����O�İ뾶Ϊ6����E��ֱ��l�ľ���Ϊ3������BD��DE��ֱ��д����BDE�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ũ���ո�С����֪1̨�����ո����3̨С���ո��1Сʱ�����ո�С��1.4���꣬2̨�����ո����5̨С���ո��1Сʱ�����ո�С��2.5���꣮
��1��ÿ̨�����ո����ÿ̨С���ո��1Сʱ�ո�С������ٹ��ꣿ
��2�������ո��ÿСʱ����Ϊ300Ԫ��С���ո��ÿСʱ����Ϊ200Ԫ�������ͺŵ��ո��һ����10̨��Ҫ��2Сʱ���8����С����ո��������ܷ��ò�����5400Ԫ���м��ַ�������ָ��������͵�һ�ַ������������Ӧ�ķ��ã�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com