
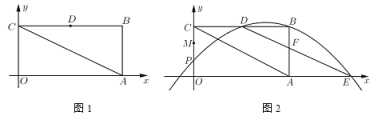
【题目】如图1,已知在平面直角坐标系![]() 中,四边形
中,四边形![]() 是矩形点
是矩形点![]() 分别在
分别在![]() 轴和
轴和![]() 轴的正半轴上,连结
轴的正半轴上,连结![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.
(1)求OC的长和点![]() 的坐标;
的坐标;
(2)如图2,![]() 是线段
是线段![]() 上的点,
上的点,![]() ,点
,点![]() 是线段
是线段![]() 上的一个动点,经过
上的一个动点,经过![]() 三点的抛物线交
三点的抛物线交![]() 轴的正半轴于点
轴的正半轴于点![]() ,连结
,连结![]() 交
交![]() 于点
于点![]()
①将![]() 沿
沿![]() 所在的直线翻折,若点
所在的直线翻折,若点![]() 恰好落在
恰好落在![]() 上,求此时
上,求此时![]() 的长和点
的长和点![]() 的坐标;
的坐标;
②以线段![]() 为边,在
为边,在![]() 所在直线的右上方作等边
所在直线的右上方作等边![]() ,当动点
,当动点![]() 从点
从点![]() 运动到点
运动到点![]() 时,点
时,点![]() 也随之运动,请直接写出点
也随之运动,请直接写出点![]() 运动路径的长.
运动路径的长.
【答案】(1) OC=![]() ,点
,点![]() 的坐标为
的坐标为![]() ;(2) ①点
;(2) ①点![]() 的坐标为
的坐标为![]() ,②
,②![]() .
.
【解析】
(1)由OA=3,tan∠OAC=![]() ,得OC=
,得OC=![]() ,由四边形OABC是矩形,得BC=OA=3,所以CD=
,由四边形OABC是矩形,得BC=OA=3,所以CD=![]() BC=
BC=![]() ,求得D(
,求得D(![]() );
);
(2)①由易知得ACB=∠OAC=30°,设将△DBF沿DE所在的直线翻折后,点B恰好落在AC上的B'处,则DB'=DB=DC,∠BDF=∠B'DF,所以∠BDB'=60°,∠BDF=∠B'DF=30°,所以BF=BDtan30°=![]() ,AF=BF=
,AF=BF=![]() ,因为∠BFD=∠AEF,所以∠B=∠FAE=90°,因此△BFD≌△AFE,AE=BD=
,因为∠BFD=∠AEF,所以∠B=∠FAE=90°,因此△BFD≌△AFE,AE=BD=![]() ,点E的坐标(
,点E的坐标(![]() ,0);
,0);
②动点P在点O时,求得此时抛物线解析式为y=![]() ,因此E(
,因此E(![]() ,0),直线DE:
,0),直线DE: ![]() ,F1(3,
,F1(3,![]() );当动点P从点O运动到点M时,求得此时抛物线解析式为
);当动点P从点O运动到点M时,求得此时抛物线解析式为![]() ,所以E(6,0),直线DE:
,所以E(6,0),直线DE:![]()
,所以F2(3,![]() );所以点F运动路径的长为
);所以点F运动路径的长为![]() ,即G运动路径的长为
,即G运动路径的长为![]() .
.
(1) ∵![]() ,
,
∴![]() .
.
∵四边形![]() 是矩形,
是矩形,
∴![]() .
.
∵![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
(2) ①∵![]() ,
,
∴![]() ,
,
∴![]() .
.
设将![]() 翻折后,点
翻折后,点![]() 落在
落在![]() 上的
上的![]() 处,
处,
则![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() ,∴点
,∴点![]() 的坐标为
的坐标为![]() .
.
②动点P在点O时,
∵抛物线过点P(0,0)、![]()
求得此时抛物线解析式为y=![]()
∴E(![]() ,0),
,0),
∴直线DE: ![]() ,
,
∴F1(3,![]() );
);
当动点P从点O运动到点M时,
∵抛物线过点
求得此时抛物线解析式为![]() ,
,
∴E(6,0),
∴直线DE:y=-![]()
∴F2(3,![]() )
)
∴点F运动路径的长为![]() ,
,
∵△DFG为等边三角形,
∴G运动路径的长为![]()


科目:初中数学 来源: 题型:
【题目】扶贫工作小组对果农进行精准扶贫,帮助果农将一种有机生态水果拓宽了市场.与去年相比,今年这种水果的产量增加了1000千克,每千克的平均批发价比去年降低了1元,批发销售总额比去年增加了![]() .
.
(1)已知去年这种水果批发销售总额为10万元,求这种水果今年每千克的平均批发价是多少元?
(2)某水果店从果农处直接批发,专营这种水果.调查发现,若每千克的平均销售价为41元,则每天可售出300千克;若每千克的平均销售价每降低3元,每天可多卖出180千克,设水果店一天的利润为![]() 元,当每千克的平均销售价为多少元时,该水果店一天的利润最大,最大利润是多少?(利润计算时,其它费用忽略不计.)
元,当每千克的平均销售价为多少元时,该水果店一天的利润最大,最大利润是多少?(利润计算时,其它费用忽略不计.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生的阅读能力,我市某校开展了“读好书,助成长”的活动,并计划购置一批图书,购书前,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,请根据统计图回答下列问题:
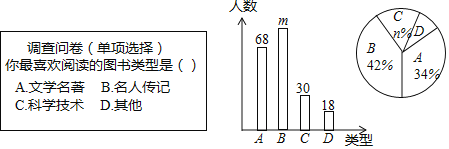
(1)本次调查共抽取了 名学生,两幅统计图中的m= ,n= .
(2)已知该校共有3600名学生,请你估计该校喜欢阅读“A”类图书的学生约有多少人?
(3)学校将举办读书知识竞赛,九年级1班要在本班3名优胜者(2男1女)中随机选送2人参赛,请用列表或画树状图的方法求被选送的两名参赛者为一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】箭头四角形,模型规律:如图1,延长CO交AB于点D,则![]() .因为凹四边形ABOC形似箭头,其四角具有“
.因为凹四边形ABOC形似箭头,其四角具有“![]() ”这个规律,所以我们把这个模型叫做“箭头四角形”.模型应用:
”这个规律,所以我们把这个模型叫做“箭头四角形”.模型应用:
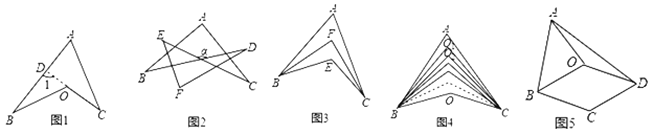
(1)直接应用:
①如图2,![]() .
.
②如图3,![]() 的2等分线(即角平分线)
的2等分线(即角平分线)![]() 交于点F,已知
交于点F,已知![]() ,则
,则![]()
③如图4,![]() 分别为
分别为![]() 的2019等分线
的2019等分线![]() .它们的交点从上到下依次为
.它们的交点从上到下依次为![]() .已知
.已知![]() ,则
,则![]() 度
度
(2)拓展应用:如图5,在四边形ABCD中,![]() .O是四边形ABCD内一点,且
.O是四边形ABCD内一点,且![]() .求证:四边形OBCD是菱形.
.求证:四边形OBCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在扇形OAB中,点C是弧AB上任意一点(不与点A,B重合),CD∥OA交OB于点D,点I是△OCD的内心,连结OI,BI.若∠AOB=β,则∠OIB等于( )

A. 180°![]() βB. 180°-βC. 90°+
βB. 180°-βC. 90°+ ![]() βD. 90°+β
βD. 90°+β
查看答案和解析>>
科目:初中数学 来源: 题型:
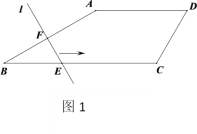
【题目】如图1,在四边形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,直线
,直线![]() .当直线
.当直线![]() 沿射线
沿射线![]() 方向,从点
方向,从点![]() 开始向右平移时,直线
开始向右平移时,直线![]() 与四边形
与四边形![]() 的边分别相交于点
的边分别相交于点![]() 、
、![]() .设直线
.设直线![]() 向右平移的距离为
向右平移的距离为![]() ,线段
,线段![]() 的长为
的长为![]() ,且
,且![]() 与
与![]() 的函数关系如图2所示,则四边形
的函数关系如图2所示,则四边形![]() 的周长是_____.
的周长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 经过点(2,3),对称轴为直线x =1.
经过点(2,3),对称轴为直线x =1.
(1)求抛物线的表达式;
(2)如果垂直于y轴的直线l与抛物线交于两点A(![]() ,
, ![]() ),B(
),B(![]() ,
, ![]() ),其中
),其中![]() ,
, ![]() ,与y轴交于点C,求BC
,与y轴交于点C,求BC![]() AC的值;
AC的值;
(3)将抛物线向上或向下平移,使新抛物线的顶点落在x轴上,原抛物线上一点P平移后对应点为点Q,如果OP=OQ,直接写出点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com