
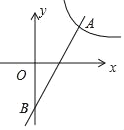
【题目】如图在平面直角坐标系xOy中,一次函数y=2x﹣2的图象与函数y=![]() (k≠0)的图象有交点为A(m,2),与y轴交于点B
(k≠0)的图象有交点为A(m,2),与y轴交于点B
(1)求反比例函数的解析式;
(2)若函数y=![]() 在第一象限的图象上有一点P,且△POB的面积为6,求点P坐标.
在第一象限的图象上有一点P,且△POB的面积为6,求点P坐标.
【答案】(1)![]() ;(2)(6,
;(2)(6,![]() ).
).
【解析】
(1)通过一次函数求出m,即求出A的坐标;然后通过把A坐标代入反比例函数,求反比例函数解析式;
(2)先确定△POB的面积以OB为底,CP为高;OB的长是固定的,只需要CP的长度;点P 在反比例函数图象上,将它代入反比例函数,从而求出P(x,![]() )即CP=x; 从而列出S△POB=
)即CP=x; 从而列出S△POB=![]() OB·
OB·![]() =
=![]() =6,即x=6,并求出y值,从而确定P的坐标;
=6,即x=6,并求出y值,从而确定P的坐标;
解:(1)由已知得点A(m,2)在函数y=2x﹣2图象上,故2m﹣2=2,解得m=2,即A(2,2)
并且点A(2,2)也在函数y=![]() 的图象上,
的图象上,
∴2=![]() 解得k=4,∴所以反比例函数y=
解得k=4,∴所以反比例函数y=![]()
(2)过点P作CP⊥y轴;△POB的面积以OB为底,CP为高;
在函数y=2x﹣2中,当x=0时,y=﹣2
即OB=2,设函数y=![]() (x>0)图象上点P(x,
(x>0)图象上点P(x,![]() )
)
∴S△POB=![]() OB·
OB·![]() =
=![]() =6
=6
解得:x=6,则y=![]()
∴此时点p(6,![]() ).
).



 能力评价系列答案
能力评价系列答案科目:初中数学 来源: 题型:
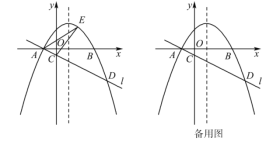
【题目】 如图所示,在平面直角坐标系xOy中,抛物线y=ax2-2ax-3a(a<0)与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:y=kx+b与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
(1)求A,B两点的坐标及抛物线的对称轴;
(2)求直线l的函数解析式(其中k,b用含a的式子表示);
(3)点E是直线l上方的抛物线上的动点,若△ACE的面积的最大值为![]() ,求a的值;
,求a的值;
(4)设P是抛物线的对称轴上的一点,点Q在抛物线上,以点A,D,P,Q为顶点的四边形能否成为矩形?若能,直接写出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
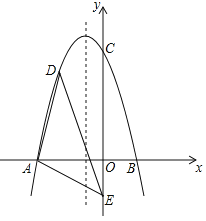
【题目】如图,在平面直角坐标系中,二次函数![]() 交
交![]() 轴于点
轴于点![]() 、
、![]() ,交
,交![]() 轴于点
轴于点![]() ,在
,在![]() 轴上有一点
轴上有一点![]() ,连接
,连接![]() .
.
(1)求二次函数的表达式;
(2)若点![]() 为抛物线在
为抛物线在![]() 轴负半轴上方的一个动点,求
轴负半轴上方的一个动点,求![]() 面积的最大值;
面积的最大值;
(3)抛物线对称轴上是否存在点![]() ,使
,使![]() 为等腰三角形,若存在,请直接写出所有
为等腰三角形,若存在,请直接写出所有![]() 点的坐标,若不存在请说明理由.
点的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的序号____.

查看答案和解析>>
科目:初中数学 来源: 题型:
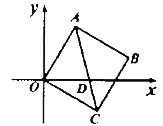
【题目】在平面直角坐标系中,边长为![]() 的正方形
的正方形![]() 的两顶点
的两顶点![]() 分别在
分别在![]() 轴、
轴、![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在原点.现将正方形
在原点.现将正方形![]() 绕
绕![]() 点顺时针旋转,
点顺时针旋转, ![]() 与
与![]() 轴相交于点
轴相交于点![]() ,如图,当
,如图,当![]() 时,点
时,点![]() 的坐标为( )
的坐标为( )
A. 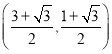 B.
B. 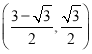 C.
C. 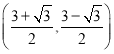 D.
D. 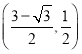
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】扶贫工作小组对果农进行精准扶贫,帮助果农将一种有机生态水果拓宽了市场.与去年相比,今年这种水果的产量增加了1000千克,每千克的平均批发价比去年降低了1元,批发销售总额比去年增加了![]() .
.
(1)已知去年这种水果批发销售总额为10万元,求这种水果今年每千克的平均批发价是多少元?
(2)某水果店从果农处直接批发,专营这种水果.调查发现,若每千克的平均销售价为41元,则每天可售出300千克;若每千克的平均销售价每降低3元,每天可多卖出180千克,设水果店一天的利润为![]() 元,当每千克的平均销售价为多少元时,该水果店一天的利润最大,最大利润是多少?(利润计算时,其它费用忽略不计.)
元,当每千克的平均销售价为多少元时,该水果店一天的利润最大,最大利润是多少?(利润计算时,其它费用忽略不计.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() .
.

(1)如图①,点![]() 在斜边
在斜边![]() 上,以点
上,以点![]() 为圆心,
为圆心,![]() 长为半径的圆交
长为半径的圆交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,与边
,与边![]() 相切于点
相切于点![]() .求证:
.求证:![]() ;
;
(2)在图②中作![]() ,使它满足以下条件:
,使它满足以下条件:
①圆心在边![]() 上;②经过点
上;②经过点![]() ;③与边
;③与边![]() 相切.
相切.
(尺规作图,只保留作图痕迹,不要求写出作法)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com