
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 上一动点,
上一动点,
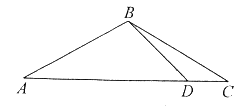
(1)![]() 的长
的长![]() ____________;
____________;
(2)![]() 的最小值是___________.
的最小值是___________.
【答案】![]() ;
; ![]()
【解析】
(1)过点B作BE⊥AC于点E,根据等腰三角形的性质得出AE=CE=![]() AC,再根据
AC,再根据![]() 利用锐角三角函数即可求得.
利用锐角三角函数即可求得.
(2)过点B作BE⊥AC于点E,延长BE到M使BE=ME,过M点作MN⊥BC于N,交AC于点D,则点D即为所求,再根据垂直平分线的性质和锐角三角函数求出MN的长即可.
(1)解:过点B作BE⊥AC于点E,
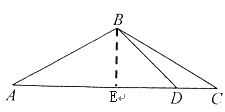
∵![]()
∴AC=2AE,
在Rt![]() ABE中,∠HEB=90°,
ABE中,∠HEB=90°,![]()
∴AE=ABcos![]() =4
=4![]() =2
=2![]() ,BE=2
,BE=2
∴AC=4![]()
故答案为:4![]() .
.
(2)过点B作BE⊥AC于点E,延长BE到M使BE=ME,过M点作MN⊥BC于N,交AC于点D,连接DB,则![]() 的最小.
的最小.

∵MN⊥BC,∴∠CND=90°,
∵![]() ,∴DN=
,∴DN=![]() CD
CD
∴![]()
∵BE⊥AC,BE=ME,
∴BD=MD,
∴![]() ,
,
∵BE⊥AC,![]()
∴∠CBM=60°,
∵BM=2BE=4,在Rt![]() BMN中,MN=BMsin60°=4
BMN中,MN=BMsin60°=4![]() =2
=2![]()
∴![]() 的最小值为2
的最小值为2![]()
故答案为:2![]()


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 交
交![]() 轴于点
轴于点![]() 、
、![]() ,交
,交![]() 轴于点
轴于点![]() ,在
,在![]() 轴上有一点
轴上有一点![]() ,连接
,连接![]() .
.
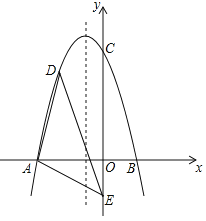
(1)求二次函数的表达式;
(2)若点![]() 为抛物线在
为抛物线在![]() 轴负半轴上方的一个动点,求
轴负半轴上方的一个动点,求![]() 面积的最大值;
面积的最大值;
(3)抛物线对称轴上是否存在点![]() ,使
,使![]() 为等腰三角形,若存在,请直接写出所有
为等腰三角形,若存在,请直接写出所有![]() 点的坐标,若不存在请说明理由.
点的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() .
.

(1)如图①,点![]() 在斜边
在斜边![]() 上,以点
上,以点![]() 为圆心,
为圆心,![]() 长为半径的圆交
长为半径的圆交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,与边
,与边![]() 相切于点
相切于点![]() .求证:
.求证:![]() ;
;
(2)在图②中作![]() ,使它满足以下条件:
,使它满足以下条件:
①圆心在边![]() 上;②经过点
上;②经过点![]() ;③与边
;③与边![]() 相切.
相切.
(尺规作图,只保留作图痕迹,不要求写出作法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生的阅读能力,我市某校开展了“读好书,助成长”的活动,并计划购置一批图书,购书前,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,请根据统计图回答下列问题:
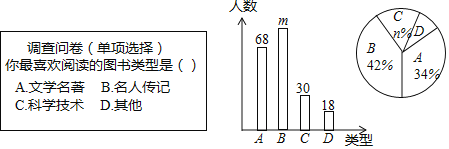
(1)本次调查共抽取了 名学生,两幅统计图中的m= ,n= .
(2)已知该校共有3600名学生,请你估计该校喜欢阅读“A”类图书的学生约有多少人?
(3)学校将举办读书知识竞赛,九年级1班要在本班3名优胜者(2男1女)中随机选送2人参赛,请用列表或画树状图的方法求被选送的两名参赛者为一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的最大值为4,且该抛物线与
的最大值为4,且该抛物线与![]() 轴的交点为
轴的交点为![]() ,顶点为
,顶点为![]() .
.
(1)求该二次函数的解析式及点![]() ,
,![]() 的坐标;
的坐标;
(2)点![]() 是
是![]() 轴上的动点,
轴上的动点,
①求![]() 的最大值及对应的点
的最大值及对应的点![]() 的坐标;
的坐标;
②设![]() 是
是![]() 轴上的动点,若线段
轴上的动点,若线段![]() 与函数
与函数![]() 的图像只有一个公共点,求
的图像只有一个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】箭头四角形,模型规律:如图1,延长CO交AB于点D,则![]() .因为凹四边形ABOC形似箭头,其四角具有“
.因为凹四边形ABOC形似箭头,其四角具有“![]() ”这个规律,所以我们把这个模型叫做“箭头四角形”.模型应用:
”这个规律,所以我们把这个模型叫做“箭头四角形”.模型应用:
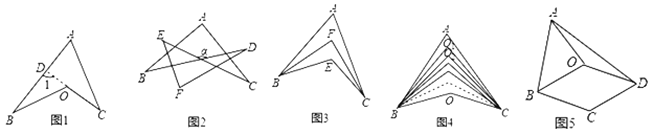
(1)直接应用:
①如图2,![]() .
.
②如图3,![]() 的2等分线(即角平分线)
的2等分线(即角平分线)![]() 交于点F,已知
交于点F,已知![]() ,则
,则![]()
③如图4,![]() 分别为
分别为![]() 的2019等分线
的2019等分线![]() .它们的交点从上到下依次为
.它们的交点从上到下依次为![]() .已知
.已知![]() ,则
,则![]() 度
度
(2)拓展应用:如图5,在四边形ABCD中,![]() .O是四边形ABCD内一点,且
.O是四边形ABCD内一点,且![]() .求证:四边形OBCD是菱形.
.求证:四边形OBCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,各个角都相等,各条边都相等的多边形叫做正多边形.对一个各条边都相等的凸多边形(边数大于3),可以由若干条对角线相等判定它是正多边形.例如,各条边都相等的凸四边形,若两条对角线相等,则这个四边形是正方形.

(1)已知凸五边形![]() 的各条边都相等.
的各条边都相等.
①如图1,若![]() ,求证:五边形
,求证:五边形![]() 是正五边形;
是正五边形;
②如图2,若![]() ,请判断五边形
,请判断五边形![]() 是不是正五边形,并说明理由:
是不是正五边形,并说明理由:
(2)判断下列命题的真假.(在括号内填写“真”或“假”)
如图3,已知凸六边形![]() 的各条边都相等.
的各条边都相等.
①若![]() ,则六边形
,则六边形![]() 是正六边形;( )
是正六边形;( )
②若![]() ,则六边形
,则六边形![]() 是正六边形. ( )
是正六边形. ( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com