
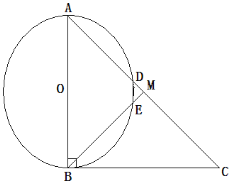
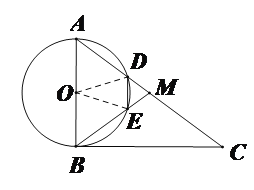
【题目】如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.
(1)求证:MD=ME
(2)填空:①若AB=6,当AD=2DM时,DE=___________;
②连接OD,OE,当∠A的度数为____________时,四边形ODME是菱形.
【答案】(1)详见解析;(2)(2)①2;②60°.
【解析】
试题分析:(1)根据直角三角形斜边的中线等于斜边的一半可得MA=MB,即可得∠A=∠MBA,再由∠ADE+∠ABE=180°,∠ADE+∠MDE=180°可得∠MDE=∠MBA.用同样的方法可得∠MDE=∠A.所以∠MDE=∠MED,即可得MD=ME.(2)①由MD=ME,又MA=MB, 可得DE∥AB,所以![]() ,又AD=2DM,即
,又AD=2DM,即![]() ,所以
,所以![]() ,可得DE=2;②当∠A=600时, △AOD是等边三角形,这时∠DOE=600, △ODE和△MDE都是等边三角形,且全等。四边形ODME是菱形。
,可得DE=2;②当∠A=600时, △AOD是等边三角形,这时∠DOE=600, △ODE和△MDE都是等边三角形,且全等。四边形ODME是菱形。
试题解析:(1)在Rt△ABC中,点M是AC的中点,
∴MA=MB,
∴∠A=∠MBA,
∵四边形ABDE是园内接四边形,
∴∠ADE+∠ABE=180°,
又因∠ADE+∠MDE=180°,
∴∠MDE=∠MBA.
同理可得∠MDE=∠A.
∴∠MDE=∠MED,
∴MD=ME.
(2)①2;②60°.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:
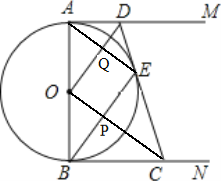
【题目】如图所示,AB是⊙O的直径,AM、BN是⊙O的两条切线,D、C分别在AM、BN上,DC切⊙O于点E,连接OD、OC、BE、AE,BE与OC相交于点P,AE与OD相交于点Q,已知AD=4,BC=9. 以下结论:
①⊙O的半径为![]() ②OD∥BE ③PB=
②OD∥BE ③PB=![]()
![]() ④tan∠CEP=
④tan∠CEP=![]()
其中正确的结论有( )
A. 1个 B. 2个 C.3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( ).
A.点P(3,-4)关于原点的对称点为P′(-3,-4)
B.点P(3,-4)关于x轴的对称点为P′(3,4)
C.点P(3,-4)关于y轴的对称点为P′(-3,-4)
D.点P(3,-2)关于原点的对称点为P′(-3,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.

(1)数轴上点A表示的数为________.
(2)将长方形OABC沿数轴水平移动,移动后的长方形记为O′A′B′C′,移动后的长方形O′A′B′C′与原长方形OABC重叠部分(如图2中阴影部分)的面积记为S.
①当S恰好等于原长方形OABC面积的一半时,数轴上点A′表示的数是多少?
②设点A的移动距离AA′=x.
(ⅰ)当S=4时,求x的值;
(ⅱ)D为线段AA′的中点,点E在线段OO′上,且OE=![]() OO′,当点D,E所表示的数互为相反数时,求x的值.
OO′,当点D,E所表示的数互为相反数时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
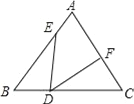
【题目】如图,△ABC中,∠B=∠C=∠EDF=α,BD=CF,BE=CD,则下列结论正确的是( )
A. 2α+∠A=180° B. α+∠A=90° C. 2α+∠A=90° D. α+∠A=180°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com