
【题目】如图,将△ABC绕点A逆时针旋转α后,与△ADE构成位似图形,我们称与互为“旋转位似图形”。
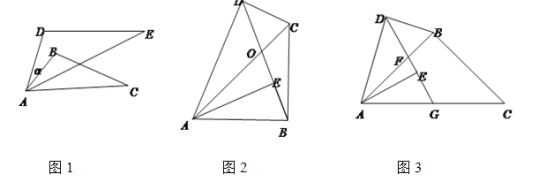
(1)知识理解:两个重合了一个顶点且边长不相等的等边三角形______(填“是”或“不是”)“旋转位似图形”;
如图1,△ABC和△ADE互为“旋转位似图形”,
①若α=26,∠B=100,∠E=29,则∠BAE=______;
②若AD=6,DE=8,AB=4,则BC=______;
(2)知识运用:
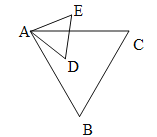
如图2,在四边形ABCD中,∠ADC=90,AE⊥BD于E,∠DAC=∠DBC,求证:△ACD和△ABE互为“旋转位似图形”;
(3)拓展提高:
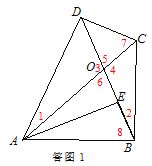
如图3,△ABC为等腰直角三角形,点G为AC中点,点F是AB上一点,D是GF延长线上一点,点E在线段GF上,且△ABD与△AGE互为“旋转位似图形”,若AC=6,AD=2![]() ,求出DE和BD的值。
,求出DE和BD的值。
【答案】(1)是 ;①25;② ![]() ;(2)答案见解析;(3)DE=2,BD=
;(2)答案见解析;(3)DE=2,BD=![]() .
.
【解析】(1)由“旋转位似图形”的定义解答即可.
(2)①由“旋转位似图形”的定义得到△ADE∽△ABC,从而可以得出∠C,∠BAC的度数,由旋转的性质可知:∠EAC=α=26°,即可得到结论.
②由相似三角形对应边成比例即可得到结论;
(2)通过证明△AOD∽△BOC,从而有△AOB∽△DOC,再由∠7=∠8,得到△ABE∽△ACD,即可得到结论;
(3)过E作EH⊥AD于H,由△ABD∽△AGE,得到AE=2.通过证明△AHE为等腰直角三角形和勾股定理,得到DE的长,由△ADB是Rt△得到BD的长.
(1)如图,△ADE和△ABC是等边三角形,∴△ADE∽△ABC,当△ADE绕点A顺时针旋转∠DAB的度数时,两个三角形位似,∴△ADE和△ABC互为“旋转位似图形”.
故答案为:是.
(2)①∵△ADE∽△ABC,∴∠E=∠C=29°,∴∠BAC=180°-100°-29°=51°,由旋转的性质可知:∠EAC=α=26°,∴∠BAE=51°-26°=25°.
故答案为:25°.
②∵△ADE∽△ABC,∴AD:DE=AB:BC,∴6:8=4:BC,解得:BC=![]() .故答案为:
.故答案为:![]() .
.
(2)如图,
∵∠1=∠2,∠3=∠4,
∴△AOD∽△BOC,∴![]() .
.
又∵∠5=∠6,
∴△AOB∽△DOC,
∴∠7=∠8,
∴△ABE∽△ACD,
∴△ACD和△ABE互为“旋转位似图形”;
(3)过E作EH⊥AD于H.如图,
∵△ABD∽△AGE,
∴![]() ,∠1=∠2.
,∠1=∠2.
∵AC=6,AD=![]() ,
,
∴AB=![]() ,AG=3,代入求得:AE=2.
,AG=3,代入求得:AE=2.
∵∠2+∠3=45,∠1=∠2,
∴∠1+∠3=45.
∵AE=2,∴AH=![]() ,
,
∴AH=AD,
∴DE=AE=2,
∴∠DEA=∠GEA=90,
∴∠ADB=∠GEA=90,
根据勾股定理,得:BD=![]() ;
;
综上所述:DE=2,BD=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图是规格为![]() 正方形网格,请在所给网格中按下列要求操作:
正方形网格,请在所给网格中按下列要求操作:

(1)在网格建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2):
(2)在第二象限内的格点上画一-点C,使点C与线段AB组成一个以AB为底边的等腰三角形,且腰长是无理数.则点C坐标是____;
(3) ![]() 的周长=____ : 面积=_ 。
的周长=____ : 面积=_ 。
(4)画出![]() 关于x轴对称的
关于x轴对称的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某奶粉每袋的标准质量为![]() 克,在质量检测中,超过标准质量
克,在质量检测中,超过标准质量![]() 克记作
克记作![]() 克,若低于标准质量
克,若低于标准质量![]() 克以上(不包括
克以上(不包括![]() 克)的,则这袋奶粉不合格,现在抽取
克)的,则这袋奶粉不合格,现在抽取![]() 袋样品进行质量检测,结果如下(单位:克):
袋样品进行质量检测,结果如下(单位:克):
袋号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
记作(克) |
|
|
|
|
|
|
|
|
|
|
(1)这![]() 袋奶粉中有哪几袋不合格?
袋奶粉中有哪几袋不合格?
(2)质量最少的是哪袋?它的实际质量是多少?
(3)这![]() 袋奶粉的平均质量是多少?
袋奶粉的平均质量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
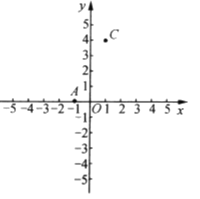
【题目】如图,![]() ,
,![]() ,点
,点![]() 在
在![]() 轴上,且
轴上,且![]() .
.
(1)求点![]() 的坐标,并画出
的坐标,并画出![]() ;
;
(2)求![]() 的面积;
的面积;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使以
,使以![]() 三点为顶点的三角形的面积为10?若存在,请直接写出点
三点为顶点的三角形的面积为10?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养鸡场有2500只鸡准备对外出售.从中随机抽取了一部分鸡,根据它们的质量(单位:![]() ),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
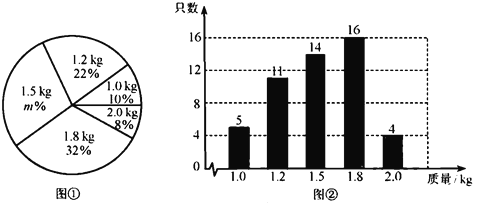
(Ⅰ)图①中![]() 的值为 ;
的值为 ;
(Ⅱ)求统计的这组数据的平均数、众数和中位数;
(Ⅲ) 根据样本数据,估计这2500只鸡中,质量为![]() 的约有多少只?
的约有多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知A.B是直线上的两点,且AB=6,若P在这条直线上,且PA=5.
①画出P点在直线AB上的大致位置图;
②求PB长.
(2)尺规作图(不写作法.保留作图痕迹)
已知线段![]() ,求作:线段MN,使MN=
,求作:线段MN,使MN=![]() .
.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
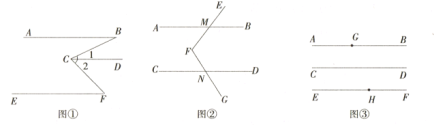
【题目】探究:如图①, ![]() ,试说明
,试说明![]() .下面给出了这道题的解题过程,请在下列解答中,填上适当的理由.
.下面给出了这道题的解题过程,请在下列解答中,填上适当的理由.
解: ∵![]() .(已知)
.(已知)
∴ ![]() .( )
.( )
同理可证, ![]() .
.
∵ ![]() ,
,
∴![]() .( )
.( )
应用:如图②, ![]() ,点
,点![]() 在
在![]() 之间,
之间,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() .若
.若![]() ,
,![]() ,则
,则![]() 的大小为_____________度.
的大小为_____________度.
拓展:如图③,直线![]() 在直线
在直线![]() 之间,且
之间,且![]() ,点
,点![]() 分别在直线
分别在直线![]() 上,点
上,点![]() 是直线
是直线![]() 上的一个动点,且不在直线
上的一个动点,且不在直线![]() 上,连结
上,连结![]() .若
.若![]() ,则
,则![]() =________度.
=________度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别在边BC,CD上,且BE=CF.连接AE,BF,AE与BF交于点G.下列结论错误的是( )
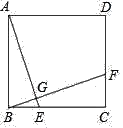
A. AE=BF B. ∠DAE=∠BFC
C. ∠AEB+∠BFC=90° D. AE⊥BF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com