
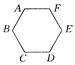
【题目】如图所示,已知六边形ABCDEF中,∠A=∠B=∠C=∠D=∠E=∠F=120°.试说明AB+BC=EF+ED.
【答案】见解析
【解析】分析:分别延长AB、DC相交于点M,延长AF、DE相交于点N,通过作辅助线我们可以得到∠MBC=∠MCB=60°,再结合三角形内角和定理即可判断△BMC是等边三角形,同理还可以得出△EFN是等边三角形;由“两组对角分别相等的四边形是平行四边形”可知四边形AMDN是平行四边形,从而可以得到AM=DN即可得出结果.
本题解析:分别延长AB、DC相交于点M,延长AF、DE相交于点N.
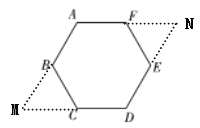
∵∠ABC=∠DCB=120°,
∴∠MBC=∠MCB=60°.
∵在△MBC中,∠MBC=∠MCB=60°,
∴∠CMB=60°.
同理∠FNE=60°.
∵∠MBC=∠MCB=60°,∠CMB=60°,
∴△BMC是等边三角形.
同理△EFN是等边三角形.
∵∠BAN=∠CDE=120°,∠CMB=60°,∠FNE=60°,
∴四边形AMDN是平行四边形,
∴AM=DN.
∵△BMC、△EFN是等边三角形,
∴BC=BM,EF=EN.
∵AM=DN,BC=BM,EF=EN,
∴AB+BC=DE+EF.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于P(x,y)作变换得到P′(﹣y+1,x+1),例如:A1(3,1)作上述变换得到A2(0,4),再将A2做上述变换得到A3___________,这样依次得到A1,A2,A3,…An;…,则A2018的坐标为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
(1)计算:3( ![]() ﹣π)0﹣
﹣π)0﹣ ![]() +(﹣1)2011
+(﹣1)2011
(2)先化简,再求值: ![]() ,其中x=
,其中x= ![]() -3.
-3.
(3)如图,平行四边形ABCD的对角线AC、BD交于点O,E、F在AC上,G、H在BD上,且AF=CE,BH=DG. 求证:GF∥HE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用1─9中的三个数字,如2、3、5组成数字不重复的三位整数,共有6个,计算方法为:3×2×1=6,现有1个老师和4个学生站成一排照相,老师站在正中间的不同站法有______种?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数的图象与反比例函数 ![]() 的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0).当x<﹣1时,一次函数值大于反比例函数值,当x>﹣1时,一次函数值小于反比例函数值.
的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0).当x<﹣1时,一次函数值大于反比例函数值,当x>﹣1时,一次函数值小于反比例函数值.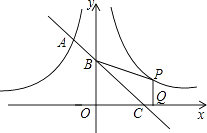
(1)求一次函数的解析式;
(2)设函数y2= ![]() 的图象与
的图象与 ![]() 的图象关于y轴对称,在y2=
的图象关于y轴对称,在y2= ![]() 的图象上取一点P(P点的横坐标大于2),过P作PQ丄x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标.
的图象上取一点P(P点的横坐标大于2),过P作PQ丄x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好地保护美丽如画的邛海湿地,西昌市污水处理厂决定先购买A,B两种型号的污水处理设备共20台,对邛海湿地周边污水进行处理.每台A型污水处理设备12万元,每台B型污水处理设备10万元.已知1台A型污水处理设备和2台B型污水处理设备每周可以处理污水640 t,2台A型污水处理设备和3台B型污水处理设备每周可以处理污水1 080 t.
(1)求A,B两种型号的污水处理设备每周每台分别可以处理污水多少吨.
(2)经预算,市污水处理厂购买设备的资金不超过230万元,每周处理污水的量不低于4 500 t,请你列举出所有购买方案,并指出哪种方案所需资金最少,最少是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点A为x轴负半轴上一点,点B为x轴正半轴上一点,C(0,a),D(b,a),其中a,b满足关系式:|a+3|+(b-a+1)2=0.
(1)a=___,b=___,△BCD的面积为______;
(2)如图2,若AC⊥BC,点P线段OC上一点,连接BP,延长BP交AC于点Q,当∠CPQ=∠CQP时,求证:BP平分∠ABC;
(3)如图3,若AC⊥BC,点E是点A与点B之间一动点,连接CE,CB始终平分∠ECF,当点E在点A与点B之间运动时,![]() 的值是否变化?若不变,求出其值;若变化,请说明理由.
的值是否变化?若不变,求出其值;若变化,请说明理由.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小英和小明姐弟二人准备一起去观看端午节龙舟赛.但因家中临时有事,必须留下一人在家,于是姐弟二人采用游戏的方式来确定谁去看龙舟赛.游戏规则是:在不透明的口袋中分别放入2个白色和1个黄色的乒乓球,它们除颜色外其余都相同.游戏时先由小英从口袋中任意摸出1个乒乓球记下颜色后放回并摇匀,再由小明从口袋中摸出1个乒乓球,记下颜色.如果姐弟二人摸到的乒乓球颜色相同.则小英赢,否则小明赢.
(1)请用树状图或列表的方法表示游戏中所有可能出现的结果.
(2)这个游戏对游戏双方公平吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com