
���� ��1���ɶ��κ�������ʽ�����öԳ��ṫʽ��������ߵĶԳ��ᣬȷ����D������꼴�ɣ�
������ƽ�ƺ�������ߵĽ���ʽΪy=-$\frac{1}{4}$x2+$\frac{3}{2}$x+k����y=0���x��ֵ��ȷ����A��B���꣬���������ľ��빫ʽ��ʾ��AB2��AC2+BC2�����ݹ��ɶ����õ�AC2+BC2=AB2���г�����k�ķ��̣�������̵Ľ�õ�k��ֵ������ȷ������ʱ�����ߵĽ���ʽ��
��������ƽ�ƺ��������ֻ��һ�������㣬�ʴ˷�����������ȵ�ʵ�������ó��б�ʽ��=4-2h��2-4��h2-4k��=0���������k��h��a�Ĺ�ϵ���ɵó����㣨h��k����ֱ��y=x-1�ϣ�
��� 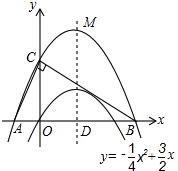 �⣺��1����y=-$\frac{1}{4}$x2+$\frac{3}{2}$x�ã�x=-$\frac{b}{2a}$=3��
�⣺��1����y=-$\frac{1}{4}$x2+$\frac{3}{2}$x�ã�x=-$\frac{b}{2a}$=3��
��D��3��0����
������ͼ����ƽ�ƺ�������ߵĽ���ʽΪy=-$\frac{1}{4}$x2+$\frac{3}{2}$x+k��
��C��0��k������OC=k��
��y=0����-$\frac{1}{4}$x2+$\frac{3}{2}$x+k=0��
��ã�x1=3+$\sqrt{4k+9}$��x2=3-$\sqrt{4k+9}$��
��A��3-$\sqrt{4k+9}$��0����B��3+$\sqrt{4k+9}$��0����
��AB2=��$\sqrt{4k+9}$+3-3+$\sqrt{4k+9}$��2=16k+36��
AC2+BC2=k2+��3-$\sqrt{4k+9}$��2+k2+��3+$\sqrt{4k+9}$��2=2k2+8k+36��
��AC2+BC2=AB2����2k2+8k+36=16k+36��
��ã�k1=4��k2=0����ȥ����
�������ߵĽ���ʽΪy=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4��
������ƽ�ƺ�������ߵĽ���ʽΪy=-$\frac{1}{4}$��x-h��2+k��
�ɲ�����Ķ��壬�÷���t=-$\frac{1}{4}$��t-h��2+k��
��t2+��4-2h��t+h2-4k=0��
��ƽ�ƺ��������ֻ��һ�������㣬
��˷�����������ȵ�ʵ������
���б�ʽ��=��4-2h��2-4��h2-4k��=0��
��1-h+k=0��
��k=h-1��
�ඥ�㣨h��k����ֱ��y=x-1�ϣ�
���� ���⿼���˶��κ������ۺϣ��õ���֪ʶ������������x��Ľ��㣬���κ��������ʣ��Լ����κ���ͼ���뼸�α任���������ն��κ��������ǽⱾ��Ĺؼ���


 ֱͨ������У�ܲ��¿�ֱͨ��Уϵ�д�
ֱͨ������У�ܲ��¿�ֱͨ��Уϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
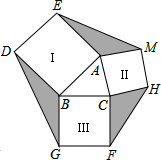 ��ͼ����֪��ABC��BC=5��AB=4���ֱ���AB��BC��CAΪ�������������Σ���ͼ����Ӱ���ֵ����֮�͵����ֵ��30��
��ͼ����֪��ABC��BC=5��AB=4���ֱ���AB��BC��CAΪ�������������Σ���ͼ����Ӱ���ֵ����֮�͵����ֵ��30���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
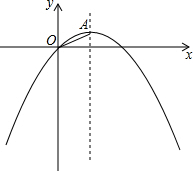 ��֪����ƽ��ֱ������ϵ�У�������y=ax2+x�ĶԳ���Ϊֱ��x=2������ΪA
��֪����ƽ��ֱ������ϵ�У�������y=ax2+x�ĶԳ���Ϊֱ��x=2������ΪA�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
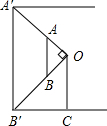 С������ѧ����ѧϰ�ˡ����������Ρ���һ�����ݺؼ�������ѧ����֪ʶȥ��������С��·�Ƶĸ߶ȣ���������һ�����Ƶ�ֱ�����ǰ���Ƥ�߶�����С����·�ƿ�ʼ���в�����ͨ���۲��֪·�Ƶ��ݵĸ߶���Ƹ˸߶�һ�£����ȣ�С����������ֱ�����ǰ��ƶ�λ�ò��۲죬ʹ���ǰ�Ķ���A��·����ߵ�A����һ�����ϣ�����B��·�Ƶ�B����һ�����ϣ�����¼�´�ʱ����λ�õ�C������Ƥ�߲������Ƹ˵�B�䵽C�ľ���Ϊ2m��С��֪���Լ�������Ϊ1.6m���۾���ͷ���ľ���ɺ��Բ��ƣ�����������������ݼ���·�Ƹ߶�A��B�䣮
С������ѧ����ѧϰ�ˡ����������Ρ���һ�����ݺؼ�������ѧ����֪ʶȥ��������С��·�Ƶĸ߶ȣ���������һ�����Ƶ�ֱ�����ǰ���Ƥ�߶�����С����·�ƿ�ʼ���в�����ͨ���۲��֪·�Ƶ��ݵĸ߶���Ƹ˸߶�һ�£����ȣ�С����������ֱ�����ǰ��ƶ�λ�ò��۲죬ʹ���ǰ�Ķ���A��·����ߵ�A����һ�����ϣ�����B��·�Ƶ�B����һ�����ϣ�����¼�´�ʱ����λ�õ�C������Ƥ�߲������Ƹ˵�B�䵽C�ľ���Ϊ2m��С��֪���Լ�������Ϊ1.6m���۾���ͷ���ľ���ɺ��Բ��ƣ�����������������ݼ���·�Ƹ߶�A��B�䣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
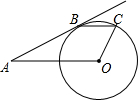 ��ͼ��AB�С�O�ڵ�B��OA=5$\sqrt{5}$��tanA=$\frac{1}{2}$����BC��OA
��ͼ��AB�С�O�ڵ�B��OA=5$\sqrt{5}$��tanA=$\frac{1}{2}$����BC��OA�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com