
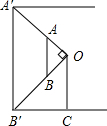
 小明在数学课上学习了“相似三角形”这一节内容后,回家想用所学到的知识去测量他家小区路灯的高度,他带上了一个自制的直角三角板与皮尺对他家小区的路灯开始进行测量,通过观察可知路灯灯泡的高度与灯杆高度一致.首先,小明手拿自制直角三角板移动位置并观察,使三角板的顶点A与路灯最高点A′在一条线上,顶点B与路灯底端B′在一条线上,并记录下此时所在位置点C,再用皮尺测量出灯杆底端B′到C的距离为2m,小明知道自己的身高为1.6m(眼睛到头顶的距离可忽略不计),请你根据以上数据计算路灯高度A′B′.
小明在数学课上学习了“相似三角形”这一节内容后,回家想用所学到的知识去测量他家小区路灯的高度,他带上了一个自制的直角三角板与皮尺对他家小区的路灯开始进行测量,通过观察可知路灯灯泡的高度与灯杆高度一致.首先,小明手拿自制直角三角板移动位置并观察,使三角板的顶点A与路灯最高点A′在一条线上,顶点B与路灯底端B′在一条线上,并记录下此时所在位置点C,再用皮尺测量出灯杆底端B′到C的距离为2m,小明知道自己的身高为1.6m(眼睛到头顶的距离可忽略不计),请你根据以上数据计算路灯高度A′B′. 分析 利用勾股定理列式求出OB′2,再求出△A′B′O与△B′OC相似,然后根据相似三角形对应边成比例列式求解即可.
解答 解:由勾股定理得,OB′2=B′C2+OC2=22+1.62=6.56,
∵A′B′⊥B′C,OC⊥B′C,
∴A′B′∥OC,
∴∠A′B′O=∠B′OC,
又∵∠A′OB′=∠OCB′=90°,
∴△A′B′O∽△B′OC,
∴$\frac{A′B′}{B′O}$=$\frac{B′O}{OC}$,
∴A′B′=$\frac{B′{O}^{2}}{OC}$=$\frac{6.56}{1.6}$=4.1米.
答:路灯高度A′B′为4.1米.
点评 本题考查了相似三角形的应用,勾股定理,主要利用了相似三角形对应边成比例的性质,确定出相似三角形并列式比例式是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
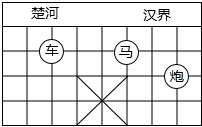 如图,已知棋子“车”的坐标为(-2,-1),棋子“马”的坐标为(1,-1),则棋子“炮”的坐标为( )
如图,已知棋子“车”的坐标为(-2,-1),棋子“马”的坐标为(1,-1),则棋子“炮”的坐标为( )| A. | (3,2) | B. | (-3,2) | C. | (3,-2) | D. | (-3,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com