
|
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
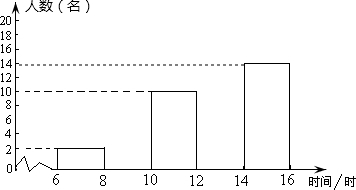 王兴喆同学为了解本校七年级500名学生“五一”放假期间参加社会实践活动的时间(单位:h),随机抽取了该年级部分学生进行了调查,并将调查结果绘制成频数分布表和频数分布直方图.请你根据图表中提供的信息,解答下列问题:
王兴喆同学为了解本校七年级500名学生“五一”放假期间参加社会实践活动的时间(单位:h),随机抽取了该年级部分学生进行了调查,并将调查结果绘制成频数分布表和频数分布直方图.请你根据图表中提供的信息,解答下列问题:| 分组 | 频数 | 百分比 |
| 6≤x<8 | 2 | 4% |
| 8≤x<10 | 6 | |
| 10≤x<12 | 10 | 20% |
| 12≤x<14 | ||
| 14≤x<16 | 28% | |
| 合计 | 50 | 100% |
查看答案和解析>>
科目:初中数学 来源: 题型:
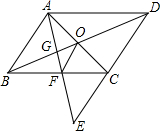 点E为平行四边形ABCD中DC边的延长线上的一点,且CE=DC,连接AE分别交BC、BD于点F、G,连接AC交BD于点O,连接OF.
点E为平行四边形ABCD中DC边的延长线上的一点,且CE=DC,连接AE分别交BC、BD于点F、G,连接AC交BD于点O,连接OF.查看答案和解析>>
科目:初中数学 来源: 题型:
 周末,小明骑自行车从家里出发到野外郊游,从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地,小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(千米)与小明离家时间x(小时)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.
周末,小明骑自行车从家里出发到野外郊游,从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地,小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(千米)与小明离家时间x(小时)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com