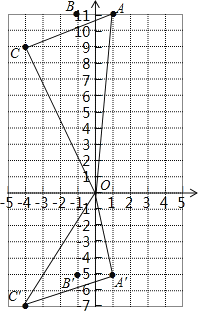
【题目】已知：
=8，则点A（1，a）关于y轴的对称点为点B，将点B向下平移2个单位后，再向左平移3个单位得到点C，则C点与原点及A点所围成的三角形的面积为多少？
【答案】13.5
【解析】
利用算术平方根的定义以及三角形面积求法和图形的平移，得出对应点坐标进而求出即可．
∵
=8，
∴a=11或-5，
∴点A（1，11）或（1，-5），
∴关于y轴的对称点为点B为（-1，11）或（-1，-5），
∵将点B向下平移2个单位后，再向左平移3个单位得到点C，
∴C（-1-3，11-2）或（-1-3，-5-2），
即：C（-4，9）或（-4，-7），
①当C（-4，9）时，与原点及x轴所围成的三角形的面积为：
S△ACO=5×11-
×2×5-×4×9-×1×11=26.5；
②当C′（-4，-7）时，与原点及x轴所围成的三角形的面积为：
S△C′OA′=5×7-×1×5-×5×2-×4×7=13.5．
科目：初中数学 来源： 题型：
【题目】数学活动问题情境：
如图1，在△ABC中，AB＝AC，∠BAC＝90°，D，E分别是边AB，AC的中点，将△ADE绕点A顺时针旋转α角（0°＜α＜90°）得到△AD′E′，连接CE′，BD′．探究CE′与BD′的数量关系；
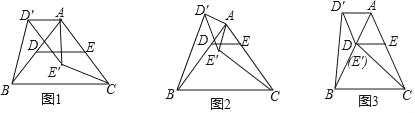
探究发展：
（1）图1中，猜想CE′与BD′的数量关系，并证明；
（2）如图2，若将问题中的条件“D，E分别是边AB，AC的中点”改为“D为AB边上任意一点，DE∥BC交AC于点E“，其他条件不变，（1）中CE′与BD′的数量关系还成立吗？请说明理由；
拓展延伸：
（3）如图3，在△ABC中，AB＝AC，∠BAC＝60°，点D，E分别在AB，AC上，且DE∥BC，将△ADE绕点A顺时针旋转60°得到△AD′E′，连接CE′，BD′，请你仔细观察，提出一个你最关心的数学问题（例如：CE′与BD′相等吗？）．
查看答案和解析>>
科目：初中数学 来源： 题型：
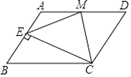
【题目】如图，在平行四边形ABCD中，点M为边AD的中点，过点C作AB的垂线交AB于点E，连接ME，已知AM＝2AE＝4，∠BCE＝30°．
（1）求平行四边形ABCD的面积S；
（2）求证：∠EMC＝2∠AEM．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知点A（a，0），B（0，b），实数a、b满足
.
（1）求点A、点B的坐标；
（2）若点P的坐标是P（－2，x），且
，且△PAB的面积为7，求x的值；
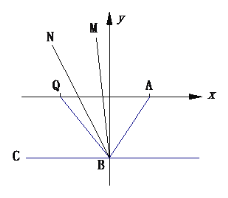
（3）如图，过点B作BC∥x轴，Q是x轴上点A左侧的一动点连接QB，BM平分∠QBA，BN平分∠ABC，当点Q运动时直接写出
____________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如右图，已知DE⊥AC，BF⊥AC，垂足分别是E、F，AE=CF，DC∥AB，
（1）试证明：DE=BF；
（2）连接DF，BE，猜想DF与BE的关系？并证明你的猜想的正确性．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某中学对全校学生进行文明礼仪知识测试，为了解测试结果，随机抽取部分学生的成绩进行分析，将成绩分为三个等级：不合格、一般、优秀，并绘制成如下两幅统计图（不完整）．
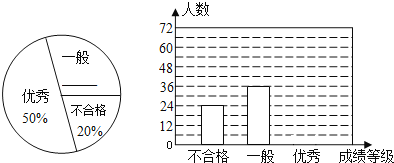
请你根据图中所给的信息解答下列问题：
（1）请将以上两幅统计图补充完整；
（2）若“一般”和“优秀”均被视为达标成绩，则该校被抽取的学生中有______人达标；
（3）若该校学生有学生 2000人，请你估计此次测试中，全校达标的学生有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知∠
是锐角，∠
是钝角，且∠
＋∠
＝180°，那么下列结论正确的是（ ）
A. ∠
的补角和∠
的补角相等 B. ∠
的余角和∠
的补角相等
C. ∠
的余角和∠
的补角互余 D. ∠
的余角和∠
的补角互补
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠A=60°，点D是BC边的中点，DE⊥BC，∠ABC的角平分线BF交DE于△ABC内一点P，连接PC．
（1）若∠ACP=24°，求∠ABP的度数；
（2）若∠ACP=m°，∠ABP=n°，请直接写出m，n满足的关系式： ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
