
【题目】数学活动问题情境:
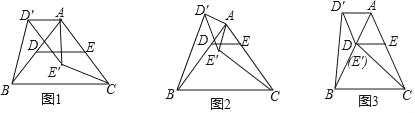
如图1,在△ABC中,AB=AC,∠BAC=90°,D,E分别是边AB,AC的中点,将△ADE绕点A顺时针旋转α角(0°<α<90°)得到△AD′E′,连接CE′,BD′.探究CE′与BD′的数量关系;
探究发展:
(1)图1中,猜想CE′与BD′的数量关系,并证明;
(2)如图2,若将问题中的条件“D,E分别是边AB,AC的中点”改为“D为AB边上任意一点,DE∥BC交AC于点E“,其他条件不变,(1)中CE′与BD′的数量关系还成立吗?请说明理由;
拓展延伸:
(3)如图3,在△ABC中,AB=AC,∠BAC=60°,点D,E分别在AB,AC上,且DE∥BC,将△ADE绕点A顺时针旋转60°得到△AD′E′,连接CE′,BD′,请你仔细观察,提出一个你最关心的数学问题(例如:CE′与BD′相等吗?).
【答案】解:(1)CE′=BD′;(2)结论不变;(3)结论:①△D′AB≌△E′AC,②△D′DB≌△DEC,③∠BD′D=∠CDE,④四边形AD′DE是菱形.(答案不唯一)
【解析】
(1)如图1中,结论:CE′=BD′.只要证明△D′AB≌△E′AC即可;
(2)结论不变,证明方法类似;
(3)结论:①△D′AB≌△E′AC,②△D′DB≌△DEC,③∠BD′D=∠CDE,④四边形AD′DE是菱形.(答案不唯一)
解:(1)如图1中,结论:CE′=BD′.
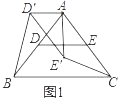
理由:∵AB=AC,AD=DB,AE=EC,
∴AD=AE,AD′=AE′,∠D′AE′=∠BAC=90°,
∴∠D′AB=∠E′AC,
在△D′AB和△′AC中,
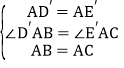 ,
,
∴△D′AB≌△E′AC,
∴BD′=CE′.
(2)如图2中,结论不变.
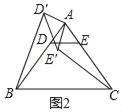
理由:∵AB=AC,
∴∠ABC=∠ACB,
∵DE∥BC,
∴∠ADE=∠ABC,∠AED=∠ACB,
∴∠ADE=∠AED,
∴AD=AE,AD′=AE′,∠D′AE′=∠BAC=90°,
∴∠D′AB=∠E′AC,
在△D′AB和△′AC中,
 ,
,
∴△D′AB≌△E′AC,
∴BD′=CE′.
(3)如图3中,结论:①△D′AB≌△E′AC,②△D′DB≌△DEC,③∠BD′D=∠CDE,④四边形AD′DE是菱形.(答案不唯一)
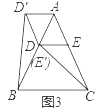
理由:∵△ADE,△AD′D,△ABC都是等边三角形,
∴D′A=AD,∥D′AB=∠DAC=60°,AB=AC,
∴△D′AB≌△DAC.
由DD′=DE,∠D′DB=∠DEC=120°.BD=EC,
可得△D′DB≌△DEC,
∴∠BD′D=∠CDE,
∵AD′=DD′=DE=AE,
∴四边形AD′DE是菱形.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=∠ABC,DE垂直平分BC,交BC于点D,交AC于点E.

(1)若AB=5,BC=8,求△ABE的周长;
(2)若BE=BA,求∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫做滑动对称变换.结合轴对称变换和平移变换的有关性质,你认为在滑动对称变换过程中,这两个对应三角形(如图)的对应点所具有的性质是( ).

A. 对应点所连线段都相等 B. 对应点所连线段被对称轴平分
C. 对应点连线与对称轴垂直 D. 对应点连线互相平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,D为AB边上任意一点,DF∥AC交BC于F,AE∥BC,∠CDE=∠ABC=∠ACB=α.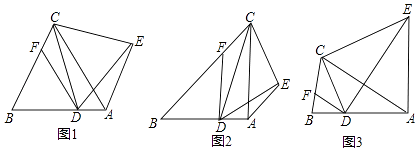
(1)如图1,当α=60°时,求证:△DCE是等边三角形.
(2)如图2.当α=45°时,求证:① ![]() =
= ![]() ;②CE⊥DE.
;②CE⊥DE.
(3)如图3,当α为任意锐角时,请直接写出线段CE与DE的数量关系(用α表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】赛龙舟是端午节的主要习俗,某市甲乙两支龙舟队在端午节期间进行划龙舟比赛,从起点A驶向终点B,在整个行程中,龙舟离开起点的距离y(米)与时间x(分钟)的对应关系如图所示,请结合图象解答下列问题: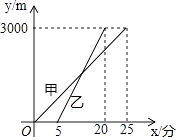
(1)起点A与终点B之间相距多远?
(2)哪支龙舟队先出发?哪支龙舟队先到达终点?
(3)分别求甲、乙两支龙舟队的y与x函数关系式;
(4)甲龙舟队出发多长时间时两支龙舟队相距200米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面内,两条直线相交时最多有1个交点,三条直线相交时最多有3个交点,四条直线相交时最多有6个交点,…,那么十条直线相交时最多有____个交点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() =8,则点A(1,a)关于y轴的对称点为点B,将点B向下平移2个单位后,再向左平移3个单位得到点C,则C点与原点及A点所围成的三角形的面积为多少?
=8,则点A(1,a)关于y轴的对称点为点B,将点B向下平移2个单位后,再向左平移3个单位得到点C,则C点与原点及A点所围成的三角形的面积为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com