
【题目】如图,△ABC中,∠A=∠ABC,DE垂直平分BC,交BC于点D,交AC于点E.

(1)若AB=5,BC=8,求△ABE的周长;
(2)若BE=BA,求∠C的度数.
【答案】(1)13(2)36°
【解析】
(1)由等边对等角可知AC=BC=8,由线段垂直平分线的性质可知CE=BE,进而可求△ABE的周长;
(2)由BE=CE可知∠C=∠CBE,由外角性质可得∠BEA=2∠C,由BE=BA可证∠A=∠BEA=2∠C,然后利用三角形内角和等于180°列式求解即可.
(1)解:∵△ABC中,∠A=∠ABC
∴AC=BC=8
∵DE垂直平分BC,
EB=EC
又∵AB=5,
∴△ABE的周长为:
AB+AE+EB=AB+(AE+EC)=AB+AC=5+8=13
(2)解:∵EB=EC
∴∠C=∠CBE
∵∠AEB=∠C+∠CBE
∴∠BEA=2∠C
∵BE=BA
∴∠AEB=∠A
又∵AC=BC
∴∠CBA=∠A=2∠C
∵∠CBA+∠A+∠C=180°
∴5∠C=180°
∴∠C=36°


科目:初中数学 来源: 题型:
【题目】△ABC中,∠A,∠B,∠C的对边分别为a、b、c,下列说法中错误的是( )
A.如果∠C-∠B=∠A,则△ABC是直角三角形,且∠C=90;
B.如果![]() ,则△ABC是直角三角形,且∠C=90;
,则△ABC是直角三角形,且∠C=90;
C.如果(c+a)( c-a)=![]() ,则△ABC是直角三角形,且∠C=90;
,则△ABC是直角三角形,且∠C=90;
D.如果∠A:∠B:∠C=3:2:5,则△ABC是直角三角形,且∠C=90.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则B6B7的边长为( )

A. 6![]() B. 12
B. 12![]() C. 32
C. 32![]() D. 64
D. 64![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.

(1)画出△ABC向右平移4个单位后得到的△A1B1C1;
(2)图中AC与A1C1的关系是: _____________.
(3)画出△ABC的AB边上的高CD;垂足是D;
(4)图中△ABC的面积是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)某酒厂每天生产A,B两种品牌的白酒共600瓶,A,B两种品牌的白酒每瓶的成本和利润如下表:设每天生产A种品牌白酒x瓶,每天获利y元.
(1)请写出y关于x的函数关系式;
(2)如果该酒厂每天至少投入成本26400元,那么每天至少获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动问题情境:
如图1,在△ABC中,AB=AC,∠BAC=90°,D,E分别是边AB,AC的中点,将△ADE绕点A顺时针旋转α角(0°<α<90°)得到△AD′E′,连接CE′,BD′.探究CE′与BD′的数量关系;
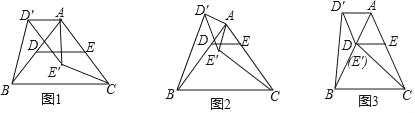
探究发展:
(1)图1中,猜想CE′与BD′的数量关系,并证明;
(2)如图2,若将问题中的条件“D,E分别是边AB,AC的中点”改为“D为AB边上任意一点,DE∥BC交AC于点E“,其他条件不变,(1)中CE′与BD′的数量关系还成立吗?请说明理由;
拓展延伸:
(3)如图3,在△ABC中,AB=AC,∠BAC=60°,点D,E分别在AB,AC上,且DE∥BC,将△ADE绕点A顺时针旋转60°得到△AD′E′,连接CE′,BD′,请你仔细观察,提出一个你最关心的数学问题(例如:CE′与BD′相等吗?).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com