
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
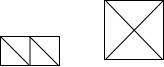 如图,将两个边长为$\sqrt{3}$的正方形对角线剪开,将所得的四个三角形拼成一个大的正方形,则这个大正方形的边长是$\sqrt{6}$.
如图,将两个边长为$\sqrt{3}$的正方形对角线剪开,将所得的四个三角形拼成一个大的正方形,则这个大正方形的边长是$\sqrt{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
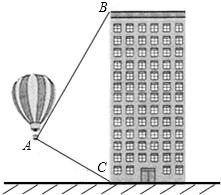 小明和小华准备利用迷你热气球来测量如图所示的高楼BC的高度,从热气球探测到此高楼顶部的仰角为66°,此高楼底部的俯角为36°,此时热气球距离C的距离是42米,请计算这栋高楼的高度是多少米(sin66°≈0.90,cos66°≈0.40,tan66°≈2.25,sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
小明和小华准备利用迷你热气球来测量如图所示的高楼BC的高度,从热气球探测到此高楼顶部的仰角为66°,此高楼底部的俯角为36°,此时热气球距离C的距离是42米,请计算这栋高楼的高度是多少米(sin66°≈0.90,cos66°≈0.40,tan66°≈2.25,sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
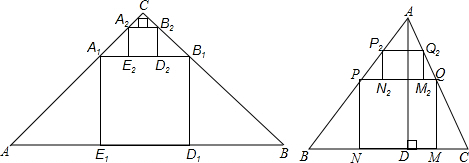
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com