
����Ŀ���������龳����ͼ�٣��ڡ�ABC�У���AB��10��AC��6����BC���ϵ�����AD��ȡֵ��Χ��
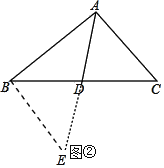
��1�������������ӳ�AD����EʹDE��AD��������BE����ACD���ŵ�D��ʱ����ת180��õ���EBD������AB��AC��2AD�����ڡ�ABE�У��������������ߵĹ�ϵ�����жϳ�����AD��ȡֵ��Χ���� ����
����˼������ʱ�������������֡��е㡱�������ߡ����������Կ��ǹ����Ը��е�Ϊ�Գ����ĵ����ĶԳ�ͼ�Σ��ѷ�ɢ����֪����������֤�Ľ��ۼ��е�ͬ���������У��Ӷ�������⣮
��2��������Ӧ�ã���ͼ�ڣ���ABC�У���BAC��90�㣬AD��BC���ϵ����ߣ��Բ����߶�AB��AC��AD֮���������ϵ����˵�����ɣ�
��3������չ���죩��ͼ�ۣ���ABC�У���BAC��90�㣬D��BC���е㣬DM��DN��DM��AB�ڵ�M��DN��AC�ڵ�N������MN����BM��4��MN��5��AC��6ʱ����ֱ��д������AD��ȡֵ��Χ��(��ܰ��ʾ:�����ֱ�������ε�����ֱ�DZ߳��ȷֱ���a��b��б�߳�����c����ô��������ѧ���Ա������߹�ϵ,a2+b2��c2)

���𰸡���1��2��AD��8 ��2���𰸼����� ��3��1��AD��7
��������
��1���ӳ�AD��E��ʹDE��AD����SAS֤����ACD�ա�EBD���ó�BE��AC��8���ڡ�ABE�У��������ε����߹�ϵ���AE��ȡֵ��Χ�����ɵó�AD��ȡֵ��Χ��
��2�����ۣ�AB2+AC2��4AD2���ӳ�AD��E��ʹDE��AD������BE����ͼ����ʾ��ֻҪ֤����ABE��90�㣬���ɹ��ɶ�������֤����
��3����ͼ���ӳ�ND��E��ʹ��DN��DE������BE��EM����취֤���ı���AMDN�Ǿ��μ��ɽ�����⣻
�⣺��1���ӳ�AD��E��ʹDE��AD������BE����ͼ����ʾ��
��AD��BC���ϵ����ߣ�
��BD��CD��
�ڡ�BDE�͡�CDA�У�
BD=CD
��BDE=��CDA
DE=AE��
���BDE�ա�CDA��SAS����
��BE��AC��6��
�ڡ�ABE�У��������ε����߹�ϵ�ã�AB��BE��AE��AB+BE��
��10��6��AE��10+6����4��AE��16��
��2��AD��8��
�ʴ�Ϊ��2��AD��8��
��2�����ۣ�AB2+AC2��4AD2��
���ɣ��ӳ�AD��E��ʹDE��AD������BE����ͼ����ʾ��
�ɣ�1����֪����BDE�ա�CDA��
��BA��AC����E����CAD��
�ߡ�BAC��90�㣬
���E+��BAE����BAE+��CAD����BAC��90�㣬
���ABE��90�㣬
��AB2+BE2��AE2��
��AB2+AC2��4AD2��
��3����ͼ���ӳ�ND��E��ʹ��DN��DE������BE��EM��
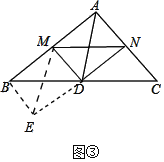
��BD��DC����BDE����CDN��DE��DN��
���BDE�ա�CDN��
��BE��CM����EBD����C��
�ߡ�ABC+��C��90�㣬
���ABD+��DBE��90�㣬
��MD��EN��DE��DN��
��ME��MN��5��
��Rt��BEM��BE��![]() ��3��
��3��
��CN��BE��3��
��AC��6��
��AN��NC��
�ߡ�BAC��90�㣬BD��DC��
��AD��DC��BD��
��DN��AC��
��Rt��AMN��AM��![]() ��4
��4
��1��AD��7


 ��Ԫ������ĩ��ϵ�д�
��Ԫ������ĩ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ֱ��AM��AN��ABƽ�֡�MAN������B��BC��BA��AN�ڵ�C������E��Dͬʱ��A����������ж���E��2cm/s���ٶ�������AN�����˶�������D��1cm/s���ٶ��˶�����֪AC��6cm���趯��D��E���˶�ʱ��Ϊt��
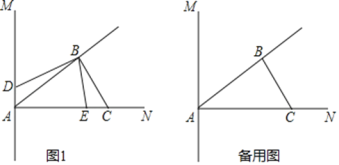
��1������D������AM���˶�ʱ����S��ADB��S��BEC��2��1�������D��E���˶�ʱ��t��ֵ��
��2��������D��ֱ��AM���˶���E������AN�˶������У��Ƿ����ij��ʱ��t��ʹ�á�ADB���BECȫ�ȣ������ڣ������ʱ��t��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ĸ�BD��CE�ཻ�ڵ�O����������һ��������ʹBD=CE���������ӵ�������________����������һ����ȵ��߶λ�һ����ȵĽǣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ������⣺
���壺���һ������ƽ�����ڣ�1����Ϊ![]() ����1�������i����������λ��������a��bi (a��bΪʵ��)������������������a�����������ʵ����b��������������鲿�����ļӣ������˷���������ʽ�ļӣ������˷��������ƣ����磬���㣺
����1�������i����������λ��������a��bi (a��bΪʵ��)������������������a�����������ʵ����b��������������鲿�����ļӣ������˷���������ʽ�ļӣ������˷��������ƣ����磬���㣺
(1��i )��(2��3i )��(1��2)��(��1��3)i��3��2i��
(1��i )��(3��i )��1��3��i��3��i��![]() ��3��(��1��3)i��1��4��2i��
��3��(��1��3)i��1��4��2i��
����������Ϣ������������⣺
��1����գ�![]() ��_______��
��_______��![]() ��________��
��________��![]() ��________��
��________��
��2�����㣺(2��i )��(1��3i )��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
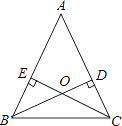
����Ŀ����ͼ����A=��B��AE=BE����D��AC���ϣ���1=��2��AE��BD�ཻ�ڵ�O��
��1����֤����AEC�ա�BED��
��2������1=40�㣬���BDE�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BC��·���½�Ϊ30������Ϊ10��һ��б�£����¶��Ƹ�CD�Ķ���D����һ̽��ƣ�����ı�Ե����DA��DB��ˮƽ·��AB���ɵļнǡ�DAN�͡�DBN�ֱ���37����60����ͼ�еĵ�A��B��C��D��M��N����ͬһƽ���ڣ�CM��AN����
��1����Ƹ�CD�ĸ߶ȣ�
��2����AB�ij��ȣ������ȷ��0.1�ף������ο����ݣ�![]() =1.73��sin37���060��cos37���0.80��tan37���0.75��
=1.73��sin37���060��cos37���0.80��tan37���0.75��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����7�֣���ͼ��ƽ���ı���ABCD�У�AB=3cm��BC=5cm����B=60����G��CD���е㣬E�DZ�AD�ϵĶ��㣬EG���ӳ�����BC���ӳ��߽��ڵ�F������CE��DF��
��1����֤���ı���CEDF��ƽ���ı��Σ�
��2������AE= cmʱ���ı���CEDF�Ǿ��Σ�
����AE= cmʱ���ı���CEDF�����Σ���ֱ��д���𰸣�����Ҫ˵�����ɣ�
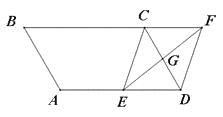
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l1��y=![]() x��ֱ��l2����A�ĺ�����Ϊ2����ֱ��l1��y������ƽ��4����λ���ȣ��õ�ֱ��l3��ֱ��l3��y�ύ�ڵ�B����ֱ��l2���ڵ�C����C��������Ϊ��2��ֱ��l2��y�ύ�ڵ�D��
x��ֱ��l2����A�ĺ�����Ϊ2����ֱ��l1��y������ƽ��4����λ���ȣ��õ�ֱ��l3��ֱ��l3��y�ύ�ڵ�B����ֱ��l2���ڵ�C����C��������Ϊ��2��ֱ��l2��y�ύ�ڵ�D��
��1����ֱ��l2�Ľ���ʽ��
��2�����BDC�������
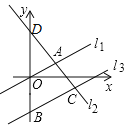
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����ȷ����ABC�ա�DEF�������ǣ� ��
A.AB=DE,BC=EF,��A=��DB.��A=��E,AB=EF,��B=��D
C.��A=��D,AB=DE,��B=��ED.��A=��D,��B=��E,��C=��F
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com