
【题目】如图①,在平面直角坐标中,边长为2的正方形OABC的两顶点A,C分别在y轴、x轴的正半轴上,O为坐标原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N.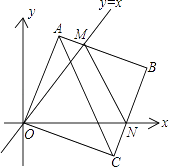
(1)当A点第一次落在直线y=x上时,求点A所经过的路线长;
(2)在旋转过程中,当MN和AC平行时,求正方形OABC旋转的度数;
(3)设△MBN的周长为p,在旋转正方形OABC的过程中,p值是否有变化?请证明你的结论.
【答案】
(1)解:∵A点第一次落在直线y=x上时停止旋转,
∴OA旋转了45°,
∴点A经过的路线长为 ![]() =
= ![]()
(2)解:∵四边形OABC是正方形,
∴∠BAC=∠BCA=45°,
当MN∥AC时,∠BMN=∠BAC=45°,∠BNM=∠BCA=45°,
∴∠BMN=∠BNM,
∴BM=BN,
∵BA=BC,
∴AM=CN,
∵OA=OC,∠OAM=∠OCN,
∴△OAM≌△OCN,
∴∠AOM=∠CON,
∵∠MON=45°,
∴∠AOM= ![]() (90°﹣45°)=22.5°,
(90°﹣45°)=22.5°,
∴旋转过程中,当MN∥AC时,正方形OABC旋转的角度为45°﹣22.5°=22.5°
(3)解:P值无变化.延长BA交y轴于E点,
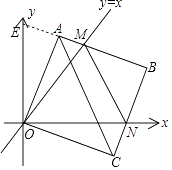
则∠AOE=45°﹣∠AOM,∠CON=90°﹣45°﹣∠AOM=45°﹣∠AOM.
∴∠AOE=∠CON,
∵OA=OC,∠OAE=180°﹣90°=90°=∠OCN,
∴△OAE≌△OCN,
∴OE=ON,AE=CN,
∵∠MOE=∠MON=45°,OM=OM,
∴△OME≌△OMN,
∴MN=ME=AM+AE,
∴MN=AM+CN,
∴P=MN+BN+BM=AM+CN+BM=AB+BC=4,
∴正方形OABC旋转过程中,P值无变化.
【解析】(1)点A经过的路线是一段弧,根据弧长公式求出圆心角的度数及半径即可求解。
(2)根据已知条件易证得△OAM≌△OCN,得出∠AOM=∠CON,即可求出∠MON、∠AOM的度数。
(3)P值无变化.延长BA交y轴于E点,先证明△OME≌△OMN,证得OM=OM,再证明△OME≌△OMN,得出MN=ME=AM+AE,即得MN=AM+CN,即可得到p的值。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上的一点,且AD∥CO. 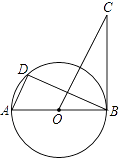
(1)求证:△ABD≌△OBC;
(2)若AB=2,BC= ![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师在黑板上写了一道题:如图1,线段AB=CD,AB与CD相交于点O,且∠AOC=60°,试比较AC+BD与AB的大小.小聪思考片刻就想出来了,他说将AB平移到CE位置,如图2,连接BE,DE,就可以比较AC+BD与AB的大小了,你知道他是怎样比较的吗?
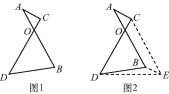
查看答案和解析>>
科目:初中数学 来源: 题型:
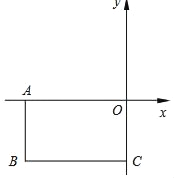
【题目】长方形OABC,O为平面直角坐标系的原点,OA=5,OC=3,点B在第三象限.
(1)求点B的坐标;
(2)如图,若过点B的直线BP与长方形OABC的边交于点P,且将长方形OABC的面积分为1:4两部分,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x=﹣3是关于x的方程(k+3)x+2=3x﹣2k的解.
(1)求k的值;
(2)在(1)的条件下,已知线段AB=6cm,点C是直线AB上一点,且BC=kAC,若点D是AC的中点,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
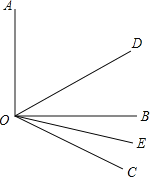
【题目】已知,如图,∠AOB=90°,∠BOC=30°,OD、OE分别是∠AOC和∠BOC的平分线.
(1)求∠COD的度数;
(2)求∠DOE的度数;
(3)若把本题的条件改成∠AOB=α,∠BOC=β,那么∠DOE的度数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,平行四边形OABC的边OC落在x轴的正半轴上,且点C(4,0),B(6,2),直线y=2x+1以每秒1个单位的速度向下平移,经过秒该直线可将平行四边形OABC的面积平分.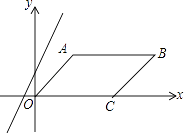
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:在平面直角坐标系![]() 中,对于任意两点
中,对于任意两点![]() 与
与![]() 的“非常距离”,给出如下定义:
的“非常距离”,给出如下定义:
若![]() ,则点
,则点![]() 与点
与点![]() 的“非常距离”为
的“非常距离”为![]() ;
;
若![]() ,则点
,则点![]() 与点
与点![]() 的“非常距离”为
的“非常距离”为![]() .
.
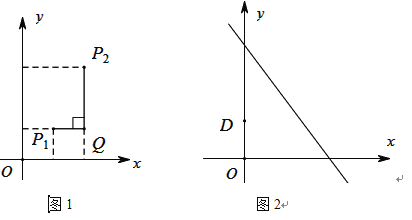
例如:点![]() ,点
,点![]() ,因为
,因为![]() ,所以点
,所以点![]() 与点
与点![]() 的“非常距离”为
的“非常距离”为![]() ,也就是图1中线段
,也就是图1中线段![]() 与线段
与线段![]() 长度的较大值(点
长度的较大值(点![]() 为垂直于
为垂直于![]() 轴的直线
轴的直线![]() 与垂直于
与垂直于![]() 轴的直线
轴的直线![]() 的交点).
的交点).
(1)已知点![]() ,
,![]() 为
为![]() 轴上的一个动点.
轴上的一个动点.
①若点![]() (0,3),则点
(0,3),则点![]() 与点
与点![]() 的“非常距离”为 ;
的“非常距离”为 ;
②若点![]() 与点
与点![]() 的“非常距离”为2,则点
的“非常距离”为2,则点![]() 的坐标为 ;
的坐标为 ;
③直接写出点![]() 与点
与点![]() 的“非常距离”的最小值为 ;
的“非常距离”的最小值为 ;
(2)已知点![]() (0,1),点
(0,1),点![]() 是直线
是直线![]() 上的一个动点,如图2,求点
上的一个动点,如图2,求点![]() 与点
与点![]() “非常距离”的最小值及相应的点
“非常距离”的最小值及相应的点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com