
| 4 |
| x |
| OM+AN |
| BN |
| OM+AN |
| BN |
| OM |
| BN |
| AN |
| BN |
| OF |
| AB |
| AF |
| AB |
| AN |
| BN |
| OM |
| BN |
| OF |
| AB |
| AN |
| BN |
| AF |
| AB |
| 4 |
| x |
| OM+AN |
| BN |
| OM |
| BN |
| OF |
| AB |
| AN |
| BN |
| AF |
| AB |
| OM+AN |
| BN |
| OM |
| BN |
| AN |
| BN |
| OF |
| AB |
| AF |
| AB |
| OA |
| AB |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 21����ͼ��ƽ��ֱ������ϵ�У���AOB�Ķ���ֱ�ΪA��2��0����O��0��0����B��0��4����
21����ͼ��ƽ��ֱ������ϵ�У���AOB�Ķ���ֱ�ΪA��2��0����O��0��0����B��0��4�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
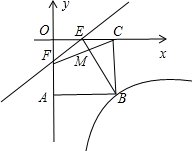
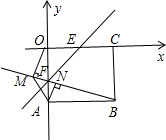
 ��ͼ��ƽ��ֱ������ϵxOy�У���A������Ϊ��2��0�����Ե�AΪԲ�ģ�2Ϊ�뾶��Բ��x�ύ��O��B���㣬CΪ��A��һ�㣬P��x���ϵ�һ�㣬����CP������A����ƽ��1����λ���ȣ���A��x�ύ��M��N����y�������ڵ�G����CP���A�����ڵ�C����CAP=60�㣮�������ƽ�ƺ�MN��PO�ij���
��ͼ��ƽ��ֱ������ϵxOy�У���A������Ϊ��2��0�����Ե�AΪԲ�ģ�2Ϊ�뾶��Բ��x�ύ��O��B���㣬CΪ��A��һ�㣬P��x���ϵ�һ�㣬����CP������A����ƽ��1����λ���ȣ���A��x�ύ��M��N����y�������ڵ�G����CP���A�����ڵ�C����CAP=60�㣮�������ƽ�ƺ�MN��PO�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ��ƽ��ֱ������ϵ�У���һ�����ֱ�����ǰ�ABC���ڵڶ����ޣ���б�������������ϣ��ҵ�A��0��2������C��-1��0������ͼ��ʾ��B��������y=ax2+ax-2�ϣ�
��ͼ��ƽ��ֱ������ϵ�У���һ�����ֱ�����ǰ�ABC���ڵڶ����ޣ���б�������������ϣ��ҵ�A��0��2������C��-1��0������ͼ��ʾ��B��������y=ax2+ax-2�ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ��ƽ��ֱ������ϵ�У�MΪx����һ�㣬��M��x����A��B���㣬��y����C��D���㣬PΪ
��ͼ��ƽ��ֱ������ϵ�У�MΪx����һ�㣬��M��x����A��B���㣬��y����C��D���㣬PΪ |
| BC |
 |
| BC |
 |
| BC |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ��ƽ��ֱ������ϵ�У�A������Ϊ��8��0����B������Ϊ��0��6��C���߶�AB���е㣮������y�����Ƿ����һ��P��ʹ����P��B��CΪ��������������AOB���ƣ������ڣ����P�����ꣻ�������ڣ�˵�����ɣ�
��ͼ��ƽ��ֱ������ϵ�У�A������Ϊ��8��0����B������Ϊ��0��6��C���߶�AB���е㣮������y�����Ƿ����һ��P��ʹ����P��B��CΪ��������������AOB���ƣ������ڣ����P�����ꣻ�������ڣ�˵�����ɣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com