练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

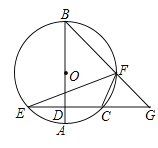
    【题目】如图，AB为⊙O的直径，C，F为⊙O上两点，过C作CD⊥AB于点D，交⊙O于点E，延长EC交BF的延长线于点G，连接CF，EG．

    （1）求证：∠BFE=∠CFG；

    （2）若FG=4，BF=6，CF=3．求EF的长．

    【答案】(1)证明见解析； (2)EF=8.

    【解析】

    （1）利用垂径定理以及等角的补角相等即可解决问题；

    （2）△GFC∽△EFB，可得，即可解决问题．

    （1）连接EB．

    ∵AB是直径，AB⊥EC，∴，∴∠BFE＝∠BEC．

    ∵∠GFC+∠BFC＝180°，∠BEC+∠BFC＝180°，∴∠CFG＝∠BEC，∴∠BFE＝∠CFG．

    （2）∵∠FCG+∠ECF＝180°，∠EBF+∠ECF＝180°，∴∠FCG＝∠EBF．

    ∵∠GFC＝∠BFE，∴△GFC∽△EFB，∴，∴，∴EF＝8．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某汽车专卖店销售A，B两种型号的新能源汽车．上周售出1辆A型车和3辆B型车，销售额为96万元；本周已售2辆A型车和1辆B型车，销售额为62万元．

    （1）求每辆A型车和B型车的售价各多少万元．

    （2）甲公司拟向该店购买A，B两种型号的新能源汽车共6辆，购车费不少于130万元，且不超过140万元. 则有哪几种购车方案?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两位同学做抛骰子（均匀正方体形状）实验，他们共抛了60次，出现向上点数的次数如表：

    向上点数

    1

    2

    3

    4

    5

    6

    出现次数

    8

    10

    7

    9

    16

    10

    （1）计算出现向上点数为6的频率．

    （2）丙说：“如果抛600次，那么出现向上点数为6的次数一定是100次．”请判断丙的说法是否正确并说明理由．

    （3）如果甲乙两同学各抛一枚骰子，求出现向上点数之和为3的倍数的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=ax2+bx+c(a≠0)与直线y=-x相交于A，B两点，则下列说法正确的是（ ）

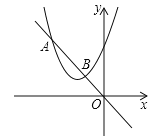
    A. ac<0，(b+1)2-4ac<0 B. ac<0，(b+1)2-4ac>0

    C. ac>0，(b+1)2-4ac<0 D. ac>0，(b+1)2-4ac>0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明和小颖上来采取以下规定决定谁将获得仅有一张科普报告入场券：在不透明的布袋里装有除颜色之外均相同的2个红球和1个绿球，小明先取出一个球，记住颜色后放回，然后小颖再取出一个球.若两次取出的球都是红色，则小明获得入场券，否则小颖获得入场券.你认为这个规则对双方公平吗？请用画树状图或列表的方法说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

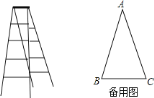
    【题目】如图，是一种用于装修的人字形梯，合拢时，梯子的长为米，距调查，这种梯子在张角为时最安全．

    （1）求梯子最安全时，梯子能达到的最大高度是多少？（精确到米）

    （2）装修时，房顶距离地面米，一个人坐在梯子最顶端时，他的手臂能达到的最大高度比梯子最顶端高出米．要使装修正常进行，那么梯子张角至多为多少度？（精确到度）

    （参考数据：，，，）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列图案中既是中心对称图形，又是轴对称图形的是（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

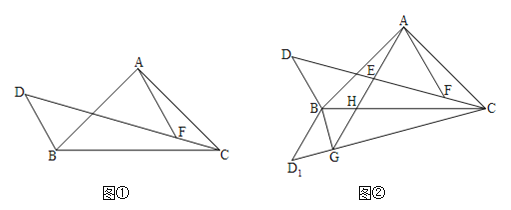
    【题目】已知△ABC，AB=AC，∠BAC=90°，D为△ABC外部一点，∠BDC=45°，点F在CD上且AF∥DB．

    （1）如图①，求证：；

    （2）如图②，将△BCD沿BC翻折得到△BCD1，过点B作BG⊥CD1，垂足为G，连接AG交CD于E，交BC于H．若AF=，∠BCD=15°，求AG的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

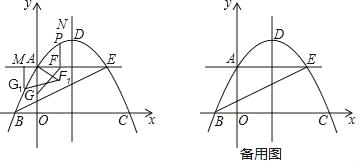
    【题目】如图，顶点为D的抛物线y＝﹣x2+x+4与y轴交于点A，与x轴交于两点B、C（点B在点C的左边），点A与点E关于抛物线的对称轴对称，点B、E在直线y＝kx+b（k，b为常数）上．

    (1)求k，b的值；

    (2)点P为直线AE上方抛物线上的任意一点，过点P作AE的垂线交AE于点F，点G为y轴上任意一点，当△PBE的面积最大时，求PF+FG+OG的最小值；

    (3)在(2)中，当PF+FG+OG取得最小值时，将△AFG绕点A按顺时方向旋转30°后得到△AF1G1，过点G1作AE的垂线与AE交于点M．点D向上平移个单位长度后能与点N重合，点Q为直线DN上任意一点，在平面直角坐标系中是否存在一点S，使以S、Q、M、N为顶点且MN为边的四边形为菱形？若存在，直接写出点S的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案