
���� ��1�����ݵ�����ϵ��������=A�ͺ�����ˮ����+B�ͺ�����ˮ�����г�y����x�ĺ�����ϵʽ��
��2����������8��֮����ɡ���A�ͺ�����ˮ��������1.8��ƿ��ȷ��������������ֵ���ɣ�
��� �⣺��1����ó����������������A�ͺ�����ˮx��ƿ��������B�ͺ�����ˮ��5-x����ƿ��
y=0.5x+0.3����5-x��=0.2x+1.5��
�����������ã�$\left\{\begin{array}{l}{\frac{x}{0.6}+\frac{5-x}{0.8}��8}\\{1.8��x��5}\end{array}\right.$��
��ã�1.8��x��4.2��
���Ա���x��ȡֵ��ΧΪ��1.8��x��4.2��
��2���ɣ�1����y=0.2x+1.5��
��k=0.2��0��
��y��x�����������
�֡�1.8��x��4.2��
�൱x=4.2ʱ��y���������=0.2��4.2+1.5=2.34��Ԫ��
��ʱ����A�ͣ�4.2��ֻ��B�ͣ�0.8��ֻ��
���� ���⿼����һ�κ�����Ӧ�ü�һԪһ�β���ʽ����Ӧ�ã�������������̼�����ʽ��⣬ѧ��Ӧ��ע������������������������һ�κ�����Ӧ�������У�Ҫע���Ա�����ȡֵ��Χ������ʹʵ�����������壮


 ��ҵ����ϵ�д�
��ҵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
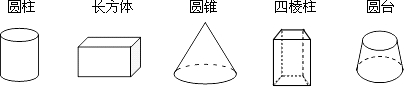
| A�� | 4�� | B�� | 3�� | C�� | 2�� | D�� | 1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
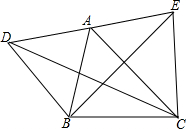 ��ͼ��AΪDE���е㣬��S1=S��DBC��S2=S��ABC��S3=S��EBC����S1��S2��S3�Ĺ�ϵ�ǣ�������
��ͼ��AΪDE���е㣬��S1=S��DBC��S2=S��ABC��S3=S��EBC����S1��S2��S3�Ĺ�ϵ�ǣ�������| A�� | S2=$\frac{3}{2}$��S1+S3�� | B�� | S2=$\frac{1}{2}$��S3-S1�� | C�� | S2=$\frac{1}{2}$��S1+S3�� | D�� | S2=$\frac{3}{2}$��S3-S1�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com