
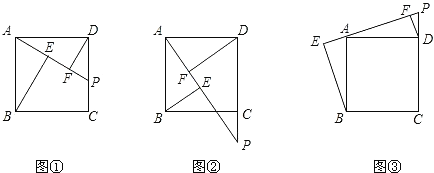
【题目】在正方形ABCD中,点P是CD边上一动点,连接PA,分别过点B、D作![]() 、
、![]() ,垂足分别为E、F.
,垂足分别为E、F.
![]() 如图
如图![]() ,请探究BE、DF、EF这三条线段的长度具有怎样的数量关系?
,请探究BE、DF、EF这三条线段的长度具有怎样的数量关系?
![]() 若点P在DC的延长线上,如图
若点P在DC的延长线上,如图![]() ,那么这三条线段的长度之间又具有怎样的数量关系?
,那么这三条线段的长度之间又具有怎样的数量关系?
![]() 若点P在CD的延长线上,如图
若点P在CD的延长线上,如图![]() ,请直接写出结论.
,请直接写出结论.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
试题(1)在图①中BE、DF、EF这三条线段长度具有这样的数量关系:BE-DF=EF,理由为:由BE垂直于AP,DF垂直于AP,得到一对直角相等,再由四边形ABCD为正方形,得到AB=AD,且∠BAD为直角,利用同角的余角相等得到一对角相等,利用AAS得到三角形ABE与三角形DFA全等,利用全等三角形对应边相等得到BE=AF,AE=DF,根据AF-AE=EF,等量代换即可得证;(2)在图②中BE、DF、EF这三条线段长度具有这样的数量关系:DF-BE=EF,理由同(1);(3)在图③中BE、DF、EF这三条线段长度具有这样的数量关系:DF+BE=EF,理由同(1).
试题解析:(1)在图①中BE、DF、EF这三条线段长度具有这样的数量关系:BE-DF=EF;
证明:∵BE⊥PA,DF⊥PA,
∴∠BEA=∠AFD=90°,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠BAE+∠DAF=90°,
又∵∠AFD=90°,
∴∠ADF+∠DAF=90°,
∴∠BAE=∠ADF,
在△BAE和△ADF中,
∴△BAE≌△ADF(AAS),
∴BE=AF,AE=DF,
∵AE-AF=EF,
∴DF-BE=EF.
(2)在图②中BE、DF、EF这三条线段长度具有这样的数量关系:DF-BE=EF;
∵BE⊥PA,DF⊥PA,
∴∠BEA=∠AFD=90°,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠BAE+∠DAF=90°,
又∵∠AFD=90°,
∴∠ADF+∠DAF=90°,
∴∠BAE=∠ADF,
在△BAE和△ADF中,
∴△BAE≌△ADF(AAS),
∴BE=AF,AE=DF,
∵AE-AF=EF,
∴DF-BE=EF.
(3)在图③中BE、DF、EF这三条线段长度具有这样的数量关系:DF+BE=EF,
理由为:∵BE⊥PA,DF⊥PA,
∴∠BEA=∠AFD=90°,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠BAE+∠DAF=90°,
又∵∠AFD=90°,
∴∠ADF+∠DAF=90°,
∴∠BAE=∠ADF,
在△BAE和△ADF中,
∴△BAE≌△ADF(AAS),
∴BE=AF,AE=DF,
∵AE+AF=EF,
∴DF+BE=EF.


科目:初中数学 来源: 题型:
【题目】如图,数轴上两定点A、B对应的数分别为-18和14,现在有甲、乙两只电子蚂蚁分别从A、B同时出发,沿着数轴爬行,速度分别为每秒1.5个单位和1.7个单位,它们第一次相向爬行1秒,第二次反向爬行2秒,第三次相向爬行3秒,第四次反向爬行4秒,第五次相向爬行5秒,……,按如此规律,则它们第一次相遇所需的时间为( )

A. 55秒 B. 190秒 C. 200秒 D. 210秒
查看答案和解析>>
科目:初中数学 来源: 题型:
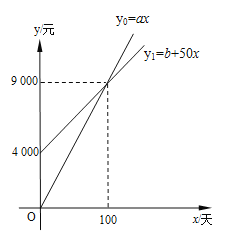
【题目】国家推行“节能减排,低碳经济”政策后,某企业推出一种“CNG”改烧汽油为天然气的装置,每辆车改装费为b元,据市场调查知:每辆车改装前、后的燃料费(含改装费)y0,y1(元)与正常运营时间x(天)之间分别满足关系式:y0=ax,y1=b+50x,图象如图所示.
(1)每辆车改装前每天的燃料费a= 元,每辆车的改装费b= 元,正常运营时间 天后,就可以从节省的燃料费中收回改装成本;
(2)某出租汽车公司一次性改装了100辆出租车,因而正常运行多少天后共节省燃料费40万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
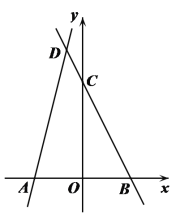
【题目】如图,在平面直角坐标系xOy中,点A(-3,0),点B在![]() 轴上,直线y=-2x+a经过点B与
轴上,直线y=-2x+a经过点B与![]() 轴交于点
轴交于点![]() (0, 6),直线AD与直线y=-2x+a相交于点D(-1,n).
(0, 6),直线AD与直线y=-2x+a相交于点D(-1,n).
(1)求直线AD的表达式;
(2)点M是直线y=-2x+a上的一点(不与点B重合),且点M的横坐标为m,求△ABM的面积S与m之间的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点M为直线AB上一动点, ![]() 都是等边三角形,连接BN
都是等边三角形,连接BN
![]() 求证:
求证: ![]() ;
;
![]() 分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系
分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系![]() 不需证明
不需证明![]() ;
;
![]() 如图4,当
如图4,当![]() 时,证明:
时,证明: ![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=4,AC=3,BC=5,DE是BC的垂直平分线,DE分别交BC、AB于点D、E.
(1)求证:△ABC为直角三角形.
(2)求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两盏路灯杆相距20米,一天晚上,当小明从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小明的身高为1.6米,那么路灯甲的高为( ) 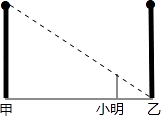
A.7米
B.8米
C.9米
D.10米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=nAD,点E,F分别在边AB,AD上且不与顶点A,B,D重合,∠AEF=∠BCE,圈O过A,E,F三点. 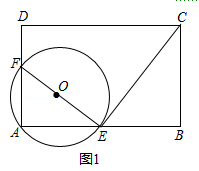
(1)求证:圈O与CE相切与点E;
(2)如图1,若AF=2FD且∠AEF=30°,求n的值; 
(3)如图2.若EF=EC且圈O与边CD相切,求n的值. 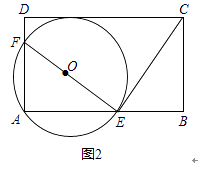
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com