练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，甲、乙两盏路灯杆相距20米，一天晚上，当小明从灯甲底部向灯乙底部直行16米时，发现自己的身影顶部正好接触到路灯乙的底部．已知小明的身高为1.6米，那么路灯甲的高为（ ）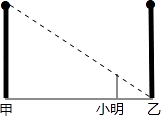
    A.7米
    B.8米
    C.9米
    D.10米

    【答案】B
    【解析】解：如图，
    ∵AB⊥OB，CD⊥OB，
    ∴△ABO∽△CDO，
    ∴ = ，
    则 = ，
    解得：AB=8，
    故选：B．
    【考点精析】掌握相似三角形的应用和中心投影是解答本题的根本，需要知道测高：测量不能到达顶部的物体的高度，通常用“在同一时刻物高与影长成比例”的原理解决；测距：测量不能到达两点间的举例，常构造相似三角形求解；手电筒、路灯和台灯的光线可以看成是从一个点发出的，这样的光线所形成的投影称为中心投影；作一物体中心投影的方法：过投影中心与物体顶端作直线，直线与投影面的交点与物体的底端之间的线段即为物体的影子．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=ax2+bx经过A（4，0），B（1，3）两点，点B、C关于抛物线的对称轴l对称，过点B作直线BH⊥x轴，交x轴于点H．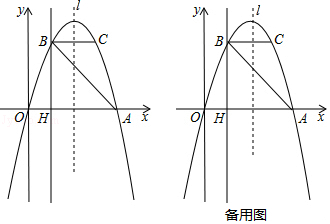

    （1）求抛物线的解析式；
    （2）若点M在直线BH上运动，点N在x轴上运动，是否存在这样的点M、N，使得以点M为直角顶点的△CNM是等腰直角三角形？若存在，请求出点M、N的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于的方程．

    求证：不论为任何实数，此方程总有实数根；

    若方程有两个不同的整数根，且为正整数，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

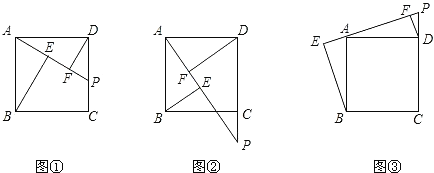
    【题目】在正方形ABCD中，点P是CD边上一动点，连接PA，分别过点B、D作、，垂足分别为E、F．

    如图，请探究BE、DF、EF这三条线段的长度具有怎样的数量关系？

    若点P在DC的延长线上，如图，那么这三条线段的长度之间又具有怎样的数量关系？

    若点P在CD的延长线上，如图，请直接写出结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列汽车标志中即是轴对称图形又是中心对称图形的是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】之前我们学习了一元一次方程的解法，下面是一道解一元一次方程的题：

    解方程﹣＝1

    老师说：这是一道含有分母的一元一次方程，我们可以根据等式的性质，可以把方程的两边同乘以6，这样就可以去掉分母了．于是，小明按照老师说的方法进行了解答，小明同学的解题过程如下：

    解：方程两边同时乘以6，得×6﹣×6＝1…………①

    去分母，得：2（2﹣3x）﹣3（x﹣5）＝1………②

    去括号，得：4﹣6x﹣3x+15＝1……………③

    移项，得：﹣6x﹣3x＝1﹣4﹣15…………④

    合并同类项，得﹣9x＝﹣18……………⑤

    系数化1，得：x＝2………………⑥

    上述小明的解题过程从第　 　步开始出现错误，错误的原因是　 　．

    请帮小明改正错误，写出完整的解题过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点E，C在BF上，，，．

    求证：；

    若AC交DE于M，且，，将线段CE绕点C顺时针旋转，使点E旋转到AB上的G处，求旋转角的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在菱形ABCD中，∠BAD=120°，将菱形沿EF折叠，点B正好落在AD边的点G处，且EG⊥AC，若CD=8，则FG的长为（ ）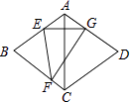
    A.4
    B.4
    C.4
    D.6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

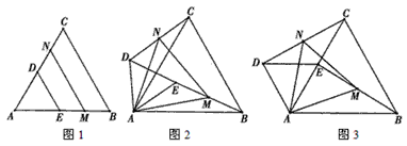
    【题目】如图，若△ABC和△ADE为等边三角形，M，N分别EB，CD的中点，易证：CD=BE，△AMN是等边三角形.

    （1）当把△ADE绕A点旋转到图2的位置时，CD=BE是否仍然成立？若成立请证明，若不成立请说明理由；

    （2）当△ADE绕A点旋转到图3的位置时，△AMN是否还是等边三角形？若是，请给出证明；若不是，请说明理由.

    查看答案和解析>>

    同步练习册答案