
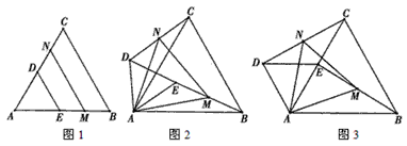
【题目】如图,若△ABC和△ADE为等边三角形,M,N分别EB,CD的中点,易证:CD=BE,△AMN是等边三角形.
(1)当把△ADE绕A点旋转到图2的位置时,CD=BE是否仍然成立?若成立请证明,若不成立请说明理由;
(2)当△ADE绕A点旋转到图3的位置时,△AMN是否还是等边三角形?若是,请给出证明;若不是,请说明理由.
【答案】(1)CD=BE.理由如下:
∵△ABC和△ADE为等边三角形
∴AB=AC,AE=AD,∠BAC=∠EAD=60o
∵∠BAE =∠BAC-∠EAC =60o-∠EAC,
∠DAC =∠DAE-∠EAC =60o-∠EAC,
∴∠BAE=∠DAC, ∴△ABE ≌ △ACD
∴CD=BE
(2)△AMN是等边三角形.理由如下:
∵△ABE ≌ △ACD, ∴∠ABE=∠ACD.
∵M、N分别是BE、CD的中点,∴BM=CN
∵AB=AC,∠ABE=∠ACD, ∴△ABM ≌ △ACN.
∴AM=AN,∠MAB=∠NAC.∴∠NAM=∠NAC+∠CAM=∠MAB+∠CAM=∠BAC=60°
∴△AMN是等边三角形.
【解析】试题分析:(1)CD=BE.利用“等边三角形的三条边相等、三个内角都是60°”的性质证得△ABE≌△ACD;然后根据全等三角形的对应边相等即可求得结论CD=BE;
(2)△AMN是等边三角形.首先利用全等三角形“△ABE≌△ACD”的对应角相等、已知条件“M、N分别是BE、CD的中点”、等边△ABC的性质证得△ABM≌△ACN;然后利用全等三角形的对应边相等、对应角相等求得AM=AN、∠NAM=∠NAC+∠CAM=∠MAB+∠CAM=∠BAC=60°,所以有一个角是60°的等腰三角形的正三角形.
解:(1)CD=BE.理由如下:
∵△ABC和△ADE为等边三角形,
∴AB=AC,AD=AE,∠BAC=∠EAD=60°,∵∠BAE=∠BAC﹣∠EAC=60°﹣∠EAC,
∠DAC=∠DAE﹣∠EAC=60°﹣∠EAC,
∴∠BAE=∠DAC,
在△ABE和△ACD中,
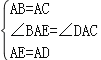 ,
,
∴△ABE≌△ACD(SAS)
∴CD=BE;
(2)△AMN是等边三角形.理由如下:
∵△ABE≌△ACD,
∴∠ABE=∠ACD.
∵M、N分别是BE、CD的中点,∴BM=CN
∵AB=AC,∠ABE=∠ACD,
在△ABM和△ACN中,
 ,
,
∴△ABM≌△ACN(SAS).
∴AM=AN,∠MAB=∠NAC.
∴∠NAM=∠NAC+∠CAM=∠MAB+∠CAM=∠BAC=60°
∴△AMN是等边三角形.


科目:初中数学 来源: 题型:
【题目】如图,甲、乙两盏路灯杆相距20米,一天晚上,当小明从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小明的身高为1.6米,那么路灯甲的高为( ) 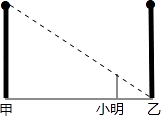
A.7米
B.8米
C.9米
D.10米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AE平分∠BAD交BC于点E.
(1)作CF平分∠BCD交AD于点F(用尺规作图,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,求证:△ABE≌△CDF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,小詹在探究筝形的性质时,得到如下结论:

①AC⊥BD;②AO=CO;③△ABD≌△CBD.
其中正确的结论有( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,每个小立方体的棱长为1,图1中共有1个立方体,其中1个看得见,0个看不见;图2中共有8个小立方体,其中7个看得见,1个看不见;图3中共有27个小立方体,其中19个看得见,8个看不见;……;则第10个图形中,其中看得见的小立方体个数是( )
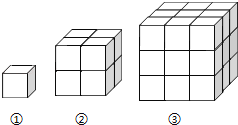
A. 270 B. 271 C. 272 D. 273
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:
如果矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形.例如,下图中的矩形A1B1C1D1 , A2B2C2D2 , AB3C3D3都是点A,B,C的覆盖矩形,其中矩形AB3C3D3是点A,B,C的最优覆盖矩形.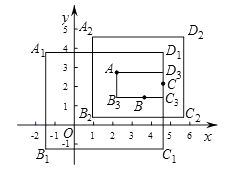
(1)已知A( ![]() 2,3),B(5,0),C(
2,3),B(5,0),C( ![]() ,
, ![]() 2).
2).
①当 ![]() 时,点A,B,C的最优覆盖矩形的面积为;
时,点A,B,C的最优覆盖矩形的面积为;
②若点A,B,C的最优覆盖矩形的面积为40,则t的值为;
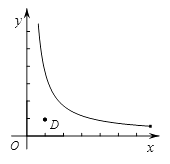
(2)已知点D(1,1),点E( ![]() ,
, ![]() ),其中点E是函数
),其中点E是函数 ![]() 的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
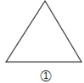
【题目】如图所示,图①是边长为1的等边三角形纸板,周长记为C1,沿图①的底边剪去一块边长为![]() 的等边三角形,得到图②,周长记为C2,然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的
的等边三角形,得到图②,周长记为C2,然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的![]() ),得图③④…,图n的周长记为Cn,若n≥3,则Cn-Cn-1=_____.
),得图③④…,图n的周长记为Cn,若n≥3,则Cn-Cn-1=_____.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,P,Q分别是BC,AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,若AQ=PQ,PR=PS,下面三个结沦:①AS=AR:②QP∥AR;③△BRP≌△CSP.其中正确的是( )
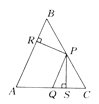
A. ①③ B. ②③ C. ①② D. ①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com