练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
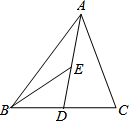
    12．如图，在△ABC中，D，E分别是BC、AD的中点，S△ABC=4，则S△ABE=（　　）
    A．2B．1C．0.5D．0.25

    分析 由图可知S△ABD和S△ABD等底等高，所以S△ABD=$\frac{1}{2}$S△ABC，同理可得S△ABE=$\frac{1}{2}$S△ABD，代入即可求出．

    解答 解：∵△ABC中，D是BC中点，
    ∴S△ABD=$\frac{1}{2}$S△ABC，
    又∵E是AD的中点，
    ∴S△ABE=$\frac{1}{2}$S△ABD，
    ∴S△ABE=$\frac{1}{4}$S△ABC，
    ∵S△ABC=4，
    ∴S△ABE=1．
    故选B．

    点评 本题考查了三角形的面积的等积变换，熟练找出相关联的底、高是解答本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2016-2017学年浙江省衢州市八年级下学期第一次月考数学试卷（解析版） 题型：解答题

    已知方程x2﹣2x﹣8=0．解决以下问题：

    （1）请按要求分别解这个方程：①配方法；②因式分解法．

    （2）①这些方法都是将解　　　　　　方程转化为解　　　　　　方程，以达到将方程降次的目的；

    ②尝试解方程：x3+2x2﹣3x=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．?ABCD中，∠A+∠C=140°，则∠C=70度，∠B=110度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．在直线l上有三点B、C、D，直线l外有一点A，若AB=10cm，AC=11cm，AD=7cm，那么A点到直线的距离（　　）
    A．等于7cmB．等于10cm
    C．不大于7cmD．大于7cm而小于11cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．线段AB=3，且AB∥x轴，若A（-2，4），则将线段向下平移4个单位长度后，点B的对应点的坐标为（　　）
    A．（1，0）B．（0，1）C．（-5，1）D．（1，0）或（-5，0）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

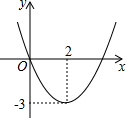    17．某同学从图中（二次函数y=ax2+bx+c）观察得出下面五条信息①a＜0，②c=0，③函数的最小值为-3，④当x＜0时，y＞0，⑤函数的对称轴为x=2，你认为其中正确的有：②③④⑤（填出序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．下列是二元一次方程的是（　　）
    A．3x=10B．2x2=yC．y+$\frac{1}{x}$=2D．x+8y=0

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年浙江省衢州市八年级下学期第一次月考数学试卷（解析版） 题型：解答题

    阅读与计算：请阅读以下材料，并完成相应的任务．

    斐波那契（约1170﹣1250）是意大利数学家，他研究了一列数，这列数非常奇妙，被称为斐波那契数列（按照一定顺序排列着的一列数称为数列）．后来人们在研究它的过程中，发现了许多意想不到的结果，在实际生活中，很多花朵（如梅花、飞燕草、万寿菊等）的瓣数恰是斐波那契数列中的数．斐波那契数列还有很多有趣的性质，在实际生活中也有广泛的应用．斐波那契数列中的第n个数可以用表示（其中，n≥1）．这是用无理数表示有理数的一个范例．

    任务：请根据以上材料，通过计算求出斐波那契数列中的第1个数和第2个数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．下列各等式成立的是（　　）
    A．$\frac{n}{n-m}$=-$\frac{n}{m+n}$B．$\frac{n}{m-n}$=-$\frac{n}{m+n}$C．$\frac{n}{n-m}$=-$\frac{-n}{m+n}$D．$\frac{n}{n-m}$=-$\frac{n}{m-n}$

    查看答案和解析>>

    同步练习册答案