
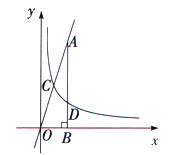
【题目】如图,反比例函数![]() (
(![]() ,)的图象与直线
,)的图象与直线![]() 相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.
相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.
(1)求k的值;
(2)求点C的坐标;
(3)在y轴上确定一点M,使点M到C、D两点距离之和d=MC+MD最小,求点M的坐标.
【答案】(1)1;(2)(![]() ,
, ![]() );(3) M(0,2
);(3) M(0,2![]() ﹣2).
﹣2).
【解析】(1)根据A坐标,以及AB=3BD求出D坐标,代入反比例解析式求出k的值;
(2)直线y=3x与反比例解析式联立方程组即可求出点C坐标;
(3)作C关于y轴的对称点C′,连接C′D交y轴于P,则P点即为所求,利用待定系数法求出直线C′D的解析式,进而可得出M点坐标.
解:A(1,3),
∴AB=3,OB=1,
∵AB=3BD,
∴BD=1,
∴D(1,1)
将D坐标代入反比例解析式得:k=1;
(2)由(1)知,k=1,
∴反比例函数的解析式为;y=![]() ,解:
,解:![]() ,
,
解得: 或
或 ,
,
∵x>0,
∴C(![]() ,
,![]() );
);
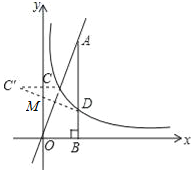
(3)如图,作C关于y轴的对称点C′,连接C′D交y轴于M,则d=MC+MD最小,
∴C′(﹣![]() ,
,![]() ),
), 
设直线C′D的解析式为:y=kx+b,
∴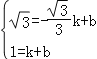 ,∴
,∴![]() ,
,
∴y=(﹣3+2![]() )x+2
)x+2![]() ﹣2,
﹣2,
当x=0时,y=2![]() ﹣2, ∴M(0,2
﹣2, ∴M(0,2![]() ﹣2).
﹣2).
“点睛”此题考查的是反比例函数综合题,涉及的知识有:坐标与图形性质,待定系数法确定函数解析式,以及直线与反比例的交点求法,熟练掌握待定系数法是解本题的关键.


科目:初中数学 来源: 题型:
【题目】给出四个命题:①若a>b,c=d,则ac>bd;②若ac>bc,则a>b;③若a>b,则ac2>bc2;④若ac2>bc2,则a>b.正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某教学活动小组选定测量小山上方某信号塔PQ的高度,他们在A处测得信号塔顶端P的仰角为45°,信号塔低端Q的仰角为31°,沿水平地面向前走100米到处,测得信号塔顶端P的仰角为68°.求信号塔PQ的高度.(结果精确到0.1米.参考数据:sin68°≈ 0.93,cos68° ≈ 0.37,tan68° ≈ 2.48,tan31° ≈ 0.60,sin31° ≈ 0.52,cos31°≈0.86)
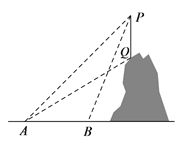
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=3,BC=10,P是BC上的动点(不与B,C重合),以A为圆心,AP长为半径作圆A,若经过点P的圆A的切线与线段AD交于点F,则以DF,BP的长为对角线长的菱形的最大面积是( )
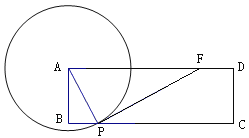
A. 4 B. 8 C. 12. 5 D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场销售甲、乙两种商品,它们的进价和售价如表,
进价(元) | 售价(元) | |
甲 | 15 | 20 |
乙 | 35 | 43 |
(1)若该商场购进甲、乙两种商品共100件,恰好用去2700元,求购进甲、乙两种商品各多少件?
(2)该商场为使销售甲、乙两种商品共100件的总利润(利润=售价﹣进价)不少于750元,且不超过760元,请你帮助该商场设计相应的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校成立“情暖校园”爱心基金会,去年上半年发给每个经济困难的学生600元,今年上半年发给了800元,设每半年发给的资金金额的平均增长率为x,则下面列出的方程中正确的是( )
A.800(1﹣x)2=600
B.600(1﹣x)2=800
C.800(1+x)2=600
D.600(1+x)2=800
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com