【题目】阅读下列材料．
让我们规定一种运算
=ad-cb，如
=2×5-3×4=-2，再如
=4x-2．按照这种运算规定，请解答下列问题．
（1）计算：
；
；
的值；
（2）当x=-1时，求
的值（要求写出计算过程）．
科目：初中数学 来源： 题型：
【题目】计算
（1）
（2）（
-
）×（-
）
（3）
（4）（-2a2）3+ a8÷a2 +3a·a5
（5）(2x-5)(2x+5)-2x(2x-3) （6）(3x+y)2-(3x-y)2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两列火车分别从A，B两城同时相向匀速驶出，甲车开往终点B城，乙车开往终点A城，乙车比甲车早到达终点；如图，是两车相距的路程d（千米）与行驶时间t（小时）的函数关系图象．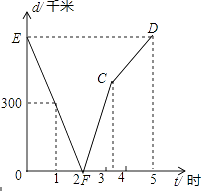 
（1）A，B两城相距千米，经过小时两车相遇；
（2）分别求出甲、乙两车的速度；
（3）直接写出甲车距A城的路程S1、乙车距A城的路程S2与t的函数关系式；（不必写出t的范围）
（4）当两车相距100千米时，求t的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场计划购进A、B两种商品，若购进A种商品20件和B种商品15件需380元；若购进A种商品15件和B种商品10件需280元．
（1）求A、B两种商品的进价分别是多少元？
（2）若购进A、B两种商品共100件，总费用不超过900元，问最多能购进A种商品多少件？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题情境：如图1，AB∥CD，∠PAB=130°，∠PCD=120°．求∠APC度数．
小明的解题思路是：如图2，过P作PE∥AB，通过平行线性质，可得∠APC=50°+60°=110°．
问题迁移：
（1）如图3，AD∥BC，点P在射线OM上运动，当点P在A、B两点之间运动时，∠ADP=∠α，∠BCP=∠β．试判断∠CPD、∠α、∠β之间有何数量关系？请说明理由；
（2）在（1）的条件下，如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你直接写出∠CPD、∠α、∠β间的数量关系．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图1，贤贤同学用手工纸制作一个台灯灯罩，请画出这个几何体的左视图和俯视图．
（2）如图2，已知直线AB与CD相交于点O，EO⊥AB，OF是∠AOC的平分线，∠EOC=
∠AOC，求∠DOF的度数．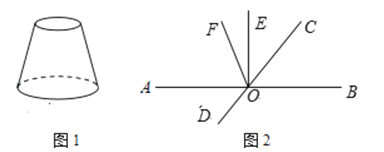
查看答案和解析>>
科目：初中数学 来源： 题型：
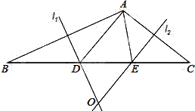
【题目】如图，在△ABC中，AB边的垂直平分线
交BC于D，AC边的垂直平分线
交BC于E， 
与
相交于点O，△ADE的周长为6cm．
（1）求BC的长；
（2）分别连结OA、OB、OC，若△OBC的周长为16cm，求OA的长；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题引入：
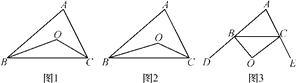
(1)如图1，在△ABC中，点O是∠ABC和∠ACB平分线的交点，若∠A＝α，则∠BOC＝ (用α表示)；
如图2，∠CBO＝
∠ABC，∠BCO＝∠ACB，∠A＝α，则∠BOC＝ (用α表示)；
拓展研究：
(2)如图3，∠CBO＝∠DBC，∠BCO＝∠ECB，∠A＝α，猜想∠BOC＝ (用α表示)，并说明理由；
(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线，它们交于点O，∠CBO＝
∠DBC，∠BCO＝∠ECB，∠A＝α，请猜想∠BOC＝ ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在数轴上，图中点A表示－36，点B表示44，动点P、Q分别从A、B两点同时出发，相向而行，动点P、Q的运动速度比之是3∶2（速度单位：1个单位长度/秒）．12秒后，动点P到达原点O，动点Q到达点C，设运动的时间为t（t＞0）秒．
（1）求OC的长；
（2）经过t秒钟，P、Q两点之间相距5个单位长度，求t的值；
（3）若动点P到达B点后，以原速度立即返回，当P点运动至原点时，动点Q是否到达A点，若到达，求提前到达了多少时间，若未能到达，说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
