
【题目】问题引入:
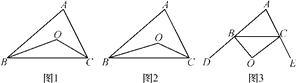
(1)如图1,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC= (用α表示);
如图2,∠CBO=![]() ∠ABC,∠BCO=
∠ABC,∠BCO=![]() ∠ACB,∠A=α,则∠BOC= (用α表示);
∠ACB,∠A=α,则∠BOC= (用α表示);
拓展研究:
(2)如图3,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,猜想∠BOC= (用α表示),并说明理由;
∠ECB,∠A=α,猜想∠BOC= (用α表示),并说明理由;
(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,请猜想∠BOC= .
∠ECB,∠A=α,请猜想∠BOC= .
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,理由见解析;(3)
,理由见解析;(3)![]() .
.
【解析】试题分析:(1)点O是∠ABC和∠ACB平分线的交点,所以∠BOC=180°-∠OBC-∠OCB=180°-![]() (∠ABC+∠ACB)=180°-
(∠ABC+∠ACB)=180°-![]() (180°-α)=
(180°-α)=![]() ;同理得图2:∠BOC=
;同理得图2:∠BOC=![]() ;(2)见解析(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,∠A=α,则∠BOC=180°-∠OBC-∠OCB=180°-
;(2)见解析(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,∠A=α,则∠BOC=180°-∠OBC-∠OCB=180°-![]() (∠DBC+∠ECB)=180°-
(∠DBC+∠ECB)=180°-![]() (180°-∠ABC+180°-∠ACB)=180°-
(180°-∠ABC+180°-∠ACB)=180°-![]() (180°+180°-∠ABC-∠ACB)= 180°-
(180°+180°-∠ABC-∠ACB)= 180°-![]() (180°+
(180°+![]() )=
)=![]() .
.
试题解析:
(1)![]() ,
,![]() ;
;
(2)![]() ,
,
理由:∵∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,
∠ECB,∠A=α,
∴∠BOC=180°-![]() (∠DBC+∠ECB)
(∠DBC+∠ECB)
=180°-![]() [360°-(∠ABC+∠ACB)]
[360°-(∠ABC+∠ACB)]
=180°-![]() [360°-(180°-∠A)]
[360°-(180°-∠A)]
=180°-![]() (180°+∠α)
(180°+∠α)
=180°-60°-![]() ∠α
∠α
=120°-![]() ∠α.;
∠α.;
(3)![]() .
.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】观察下图回答问题: 
(1)指出小明的作业从哪一步开始出现的错误,请更正过来,并计算出正确结果;
(2)若a,b是不等式组 ![]() 的整数解(a<b),求上题{}分式的值.
的整数解(a<b),求上题{}分式的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料.
让我们规定一种运算![]()
![]() =ad-cb,如
=ad-cb,如![]()
![]() =2×5-3×4=-2,再如
=2×5-3×4=-2,再如![]()
![]() =4x-2.按照这种运算规定,请解答下列问题.
=4x-2.按照这种运算规定,请解答下列问题.
(1)计算:![]()
![]() ;
;![]()
![]() ;
;![]()
![]() 的值;
的值;
(2)当x=-1时,求![]()
![]() 的值(要求写出计算过程).
的值(要求写出计算过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用若干个大小相同的小立方块搭一个几何体,使得从正面和从上面看到的这个几何体的形状如图所示
(1)请画出一种从左面看到的它的形状图;
(2)根据你所画出的从左面看到的形状图,结合从正面和从上面看到的这个几何体的形状图直接写出这个几何体所需要的小立方体的个数.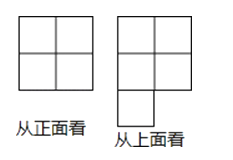
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,夜晚,小亮从点A经过路灯C的正下方沿直线走到点B,他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间的函数关系的图象大致为( )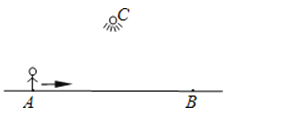
A.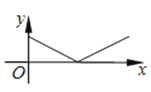
B.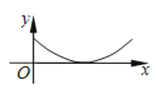
C.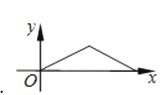
D.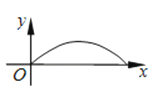
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一颗大树,它的影子是MN.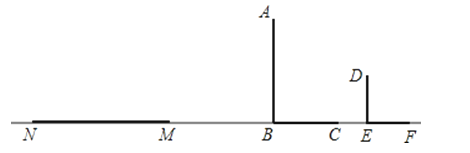
(1)试判断是路灯还是太阳光产生的影子,如果是路灯产生的影子确定路灯的位置(用点P表示).如果是太阳光请画出光线.
(2)在图中画出表示大树高的线段.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com