
【题目】如图,夜晚,小亮从点A经过路灯C的正下方沿直线走到点B,他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间的函数关系的图象大致为( )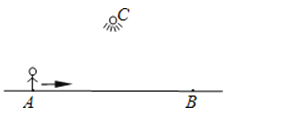
A.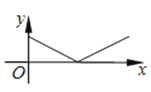
B.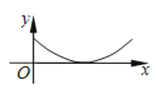
C.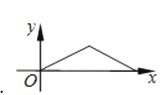
D.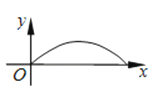
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B的坐标为(18,6).
(1)求直线l1,l2对应的函数表达式;
(2)点C为线段OB上一动点(点C不与点O,B重合),作CD∥y轴交直线l2于点D,设点C的纵坐标为a,求点D的坐标(用含a的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数.
小明的解题思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC=50°+60°=110°.
问题迁移:
(1)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.试判断∠CPD、∠α、∠β之间有何数量关系?请说明理由;


(2)在(1)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.


查看答案和解析>>
科目:初中数学 来源: 题型:
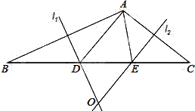
【题目】如图,在△ABC中,AB边的垂直平分线![]() 交BC于D,AC边的垂直平分线
交BC于D,AC边的垂直平分线![]() 交BC于E,
交BC于E, ![]() 与
与![]() 相交于点O,△ADE的周长为6cm.
相交于点O,△ADE的周长为6cm.
(1)求BC的长;
(2)分别连结OA、OB、OC,若△OBC的周长为16cm,求OA的长;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班部分学生接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了如图①②两幅不完整的统计图,请根据图中的信息解答下列问题.
(1)九年级(1)班接受调查的学生共有多少名?
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
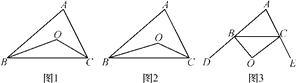
【题目】问题引入:
(1)如图1,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC= (用α表示);
如图2,∠CBO=![]() ∠ABC,∠BCO=
∠ABC,∠BCO=![]() ∠ACB,∠A=α,则∠BOC= (用α表示);
∠ACB,∠A=α,则∠BOC= (用α表示);
拓展研究:
(2)如图3,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,猜想∠BOC= (用α表示),并说明理由;
∠ECB,∠A=α,猜想∠BOC= (用α表示),并说明理由;
(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,请猜想∠BOC= .
∠ECB,∠A=α,请猜想∠BOC= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国有五座名山,但在洪雅人的心目中,我国有六座名山,这六座名山的海拔分别为:
山名 | 泰山 | 华山 | 黄山 | 庐山 | 峨嵋山 | 瓦屋山 |
海拔(米) | 1152 | 1997 | 1873 | 1500 | 1309 | 2830 |
(1)海拔最高的山是多少,最高的山与最低的山的海拔相差多少米;
(2)海拔不低于1500米的山的频数是多少;频率是多少;
(3)根据数据制作条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生对安全知识的掌握情况,学校随机抽取了20名学生进行安全知识测试,测试成绩(百分制)如下:
78、86、93、81、97、88、79、93、87、90、93、98、88、81、94、95、81、98、99、94
(1)根据上述数据,将下列表格补充完整(每组含最小值):
成绩/分 | 70~80 | 80~90 | 90~100 |
人数 | 7 |
(2)若用(1)中数据制作扇形统计图,求出表示“70~80”扇形的圆心角度数;
(3)已知该校共有2000名学生,若规定成绩90分及以上为优秀,估计该校学生对安全知识掌握情况为优秀的有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com