
【题目】如图,⊙O为△ABC的内切圆,D、E、F分别为切点,已知∠C=90°,⊙O半径长为3cm,AC=10cm,则AD长度为cm.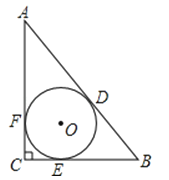
科目:初中数学 来源: 题型:
【题目】某商场计划购进A、B两种商品,若购进A种商品20件和B种商品15件需380元;若购进A种商品15件和B种商品10件需280元.
(1)求A、B两种商品的进价分别是多少元?
(2)若购进A、B两种商品共100件,总费用不超过900元,问最多能购进A种商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题引入:
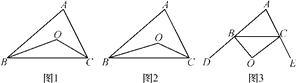
(1)如图1,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC= (用α表示);
如图2,∠CBO=![]() ∠ABC,∠BCO=
∠ABC,∠BCO=![]() ∠ACB,∠A=α,则∠BOC= (用α表示);
∠ACB,∠A=α,则∠BOC= (用α表示);
拓展研究:
(2)如图3,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,猜想∠BOC= (用α表示),并说明理由;
∠ECB,∠A=α,猜想∠BOC= (用α表示),并说明理由;
(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,请猜想∠BOC= .
∠ECB,∠A=α,请猜想∠BOC= .
查看答案和解析>>
科目:初中数学 来源: 题型:
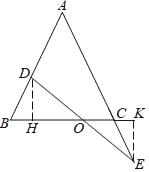
【题目】如图,△ABC中,AB=AC,D、E分别是AB及AC延长线上的点,且BD=CE,连接DE交BC于点O.过点D作DH⊥BC,过E作EK⊥BC,垂足分别为H、K.
(1)求证:DH=EK;
(2)求证:DO=EO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义运算a![]() b=a(1-b),下面给出了关于这种运算的四个结论:
b=a(1-b),下面给出了关于这种运算的四个结论:
①2![]() (-2)=6 ②a
(-2)=6 ②a![]() b=b
b=b![]() a
a
③若a+b=0,则(a![]() a)+(b
a)+(b![]() b)=2ab ④若a
b)=2ab ④若a![]() b=0,则a=0.
b=0,则a=0.
其中正确结论的序号是 (填上你认为所有正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,图中点A表示-36,点B表示44,动点P、Q分别从A、B两点同时出发,相向而行,动点P、Q的运动速度比之是3∶2(速度单位:1个单位长度/秒).12秒后,动点P到达原点O,动点Q到达点C,设运动的时间为t(t>0)秒.
(1)求OC的长;
(2)经过t秒钟,P、Q两点之间相距5个单位长度,求t的值;
(3)若动点P到达B点后,以原速度立即返回,当P点运动至原点时,动点Q是否到达A点,若到达,求提前到达了多少时间,若未能到达,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知P为⊙O外一点,PA,PB为⊙O的切线,A、B为切点,∠P=70°,C为⊙O上一个动点,且不与A、B重合,则∠BCA=( )
A.35°、145°
B.110°、70°
C.55°、125°
D.110°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解八年级学习体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A、B、C、D四个等级.请根据两幅统计图中的信息回答下列问题:


(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com