
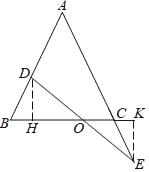
【题目】如图,△ABC中,AB=AC,D、E分别是AB及AC延长线上的点,且BD=CE,连接DE交BC于点O.过点D作DH⊥BC,过E作EK⊥BC,垂足分别为H、K.
(1)求证:DH=EK;
(2)求证:DO=EO.
【答案】(1)见解析;(2)见解析.
【解析】
(1)只要证明△BDH≌△CEK,即可解决问题;
(2)只要证明△DHO≌△EKO即可解决问题;
(1)∵DH⊥BC,EK⊥BC,
∴∠DHB=∠K=90°,
∵AB=AC,
∴∠B=∠ACB,
又∵∠ACB=∠ECK,
∴∠B=∠ECK,
在△BDH和△CEK中
∵∠ACB=∠ECK,∠B=∠ECK,BD=CE
∴△BDH≌△CEK(AAS).
∴DH=EK.
(2)∵DH⊥AC,EK⊥BC,
∴∠DHO=∠K=90°,
由(1)得EK=DH,
在△DHO和△EKO中,
∵∠DHO=∠K,∠DOH=∠EOK,DH=EK
∴△DHO≌△EKO(AAS),
∴DO=EO.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】如图,给出下列四个条件,AB=DE,BC=EF,∠B=∠E,∠C=∠F,从中任选三个条件能使△ABC≌△DEF的共有( )

A. 1组 B. 2组 C. 3组 D. 4组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用若干个大小相同的小立方块搭一个几何体,使得从正面和从上面看到的这个几何体的形状如图所示
(1)请画出一种从左面看到的它的形状图;
(2)根据你所画出的从左面看到的形状图,结合从正面和从上面看到的这个几何体的形状图直接写出这个几何体所需要的小立方体的个数.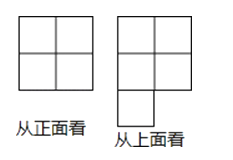
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一颗大树,它的影子是MN.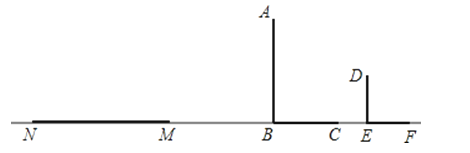
(1)试判断是路灯还是太阳光产生的影子,如果是路灯产生的影子确定路灯的位置(用点P表示).如果是太阳光请画出光线.
(2)在图中画出表示大树高的线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB.
求证:CA+AD=BC.
小明为解决上面的问题作了如下思考:作△ADC关于直线CD的对称图形△A′DC,
∵CD平分∠ACB,∴A′点落在CB上,且CA′=CA,A′D=AD.因此,要证的问题转化为只要证A′D=A′B.请根据小明的思考写出该问题完整的证明过程.
(2)参照(1)中小明的思考方法,解答下列问题:
如图3,在四边形ABCD中,AC平分∠BAD,BC=CD=10,AC=17,AD=9,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由一个边长为a的小正方形与两个长、宽分别为a,b的小长方形拼接成大长方形ABCD,则整个图形可表达出一些有关多项式因式分解的等式,请你写出其中任意三个等式:__________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)请判断BD、CE有何大小、位置关系,并证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com