
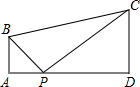
 如图,四边形ABCD中,AB∥CD,∠A=∠D=90°,AD=7,AB=2,DC=3,P为AD上一点,以P,A,B为顶点的三角形与以P,D,C为顶点的三角形相似,那么这样的点P有几个?为什么?
如图,四边形ABCD中,AB∥CD,∠A=∠D=90°,AD=7,AB=2,DC=3,P为AD上一点,以P,A,B为顶点的三角形与以P,D,C为顶点的三角形相似,那么这样的点P有几个?为什么? 分析 设AP=x,则PD=AD-AP=7-x,然后分类讨论:若∠APB=∠DPC,则Rt△APB∽Rt△DPC,得到$\frac{AP}{PD}$=$\frac{AB}{CD}$,即$\frac{x}{7-x}$=$\frac{2}{3}$;若∠APB=∠PCD,则Rt△APB∽Rt△DCP,得到$\frac{AP}{CD}$=$\frac{AB}{PD}$,即$\frac{x}{3}$=$\frac{2}{7-x}$,再分别解关于x的方程求出x的值,则可确定P点的位置.
解答 解:设AP=x,则PD=AD-AP=7-x,
若∠APB=∠DPC,则Rt△APB∽Rt△DPC,
所以$\frac{AP}{PD}$=$\frac{AB}{CD}$,即$\frac{x}{7-x}$=$\frac{2}{3}$,解得x=$\frac{14}{5}$;
若∠APB=∠PCD,则Rt△APB∽Rt△DCP,
所以$\frac{AP}{CD}$=$\frac{AB}{PD}$,即$\frac{x}{3}$=$\frac{2}{7-x}$,解得x1=1,x2=6,
所以当AP=$\frac{14}{5}$或1或6时,以P,A,B为顶点的三角形与以P,D,C为顶点的三角形相似,即这样的P点有三个.
点评 本题考查了相似三角形的判定:有两组角对应相等的两个三角形相似.也考查了分类讨论的思想.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
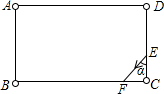 如图,矩形台球桌ABCD,其中A、B、C、D处有球洞,已知DE=4,CE=2,BC=6$\sqrt{3}$,球从E点出发,与DC夹角为α,经过BC、AB、AD三次反弹后回到E点,求tanα的取值范围( )
如图,矩形台球桌ABCD,其中A、B、C、D处有球洞,已知DE=4,CE=2,BC=6$\sqrt{3}$,球从E点出发,与DC夹角为α,经过BC、AB、AD三次反弹后回到E点,求tanα的取值范围( )| A. | $\sqrt{3}$≤tanα<$\frac{3}{2}$$\sqrt{3}$ | B. | $\frac{3\sqrt{3}}{4}$<tanα<$\frac{3}{2}$$\sqrt{3}$ | C. | tanα=$\sqrt{3}$ | D. | $\frac{3\sqrt{3}}{4}$<tanα<3$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com