
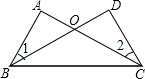
 如图,AB=CD,AC=BD,求证:∠A=∠D,∠1=∠2.
如图,AB=CD,AC=BD,求证:∠A=∠D,∠1=∠2.  开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:解答题
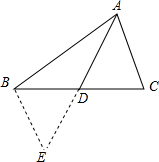 如图,AD为△ABC的中线,已知AD=4cm,试确定AB+AC的取值范围.
如图,AD为△ABC的中线,已知AD=4cm,试确定AB+AC的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
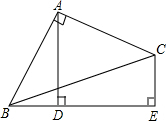 如图,在四边形ABEC中,AB=AC,∠BAC=∠E=90°,AD⊥BE于D.
如图,在四边形ABEC中,AB=AC,∠BAC=∠E=90°,AD⊥BE于D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
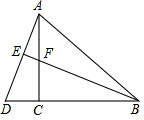 如图,在△ABC中,AC=BC,∠ACB=90°,延长BC到D,使BD=BA,BE⊥AD于点E,交AC于点F.
如图,在△ABC中,AC=BC,∠ACB=90°,延长BC到D,使BD=BA,BE⊥AD于点E,交AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
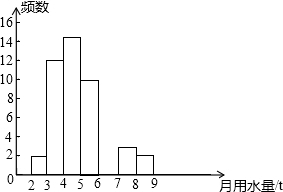 小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).| 月均用水量(单位:t) | 频数 | 百分比 |
| 2≤x<3 | 2 | 4% |
| 3≤x<4 | 12 | 24% |
| 4≤x<5 | 15 | 30% |
| 5≤x<6 | 10 | 20% |
| 6≤x<7 | 6 | 12% |
| 7≤x<8 | 3 | 6% |
| 8≤x<9 | 2 | 4% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com