
【题目】如图,AB是⊙O的一条弦,且AB=![]() .点C,E分别在⊙O上,且OC⊥AB于点D,∠E=30°,连接OA.
.点C,E分别在⊙O上,且OC⊥AB于点D,∠E=30°,连接OA.
(1)求OA的长;
(2)若AF是⊙O的另一条弦,且点O到AF的距离为![]() ,直接写出∠BAF的度数.
,直接写出∠BAF的度数.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
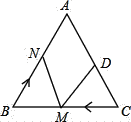
【题目】如图,在等边△ABC中,AB=AC=BC=10厘米,DC=4厘米.如果点M以3厘米/秒的速度运动.
(1)如果点M在线段CB上由点C向点B运动,点N在线段BA上由B点向A点运动.它们同时出发,若点N的运动速度与点M的运动速度相等.
①经过2秒后,△BMN和△CDM是否全等?请说明理由.
②当两点的运动时间为多少时,△BMN是一个直角三角形?
(2)若点N的运动速度与点M的运动速度不相等,点N从点B出发,点M以原来的运动速度从点C同时出发,都顺时针沿△ABC三边运动,经过25秒点M与点N第一次相遇,则点N的运动速度是 厘米/秒.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式计算正确的是( )
A.2a2+3a2=5a4
B.(﹣2ab)3=﹣6ab3
C.(3a+b)(3a﹣b)=9a2﹣b2
D.a3(﹣2a)=﹣2a3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)﹣4÷ ![]() ﹣(﹣
﹣(﹣ ![]() )×(﹣30)
)×(﹣30)
(2)﹣20+(﹣14)﹣(﹣18)﹣13
(3)﹣22+|5﹣8|+24÷(﹣3)× ![]()
(4)﹣5m2n+4mn2﹣2mn+6m2n+3mn.
查看答案和解析>>
科目:初中数学 来源: 题型:
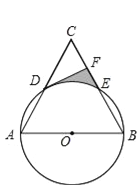
【题目】已知:如图,以等边三角形ABC一边AB为直径的⊙O与边AC、BC分别交于点D、E,过点D作DF⊥BC,垂足为F.
(1)求证:DF为⊙O的切线;
(2)若等边三角形ABC的边长为4,求DF的长;
(3)写出求图中阴影部分的面积的思路.(不求计算结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC,交AB于E,则下列结论一定正确的是( )
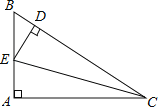
A. AE=BE B. DB=DE C. AE=BD D. ∠BCE=∠ACE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com