
【题目】一座桥如图,桥下水面宽度AB是20米,高CD是4米.要使高为3米的船通过,则其宽度须不超过多少米.
(1)如图1,若把桥看做是抛物线的一部分,建立如图坐标系.
①求抛物线的解析式;
②要使高为3米的船通过,则其宽度须不超过多少米?
(2)如图2,若把桥看做是圆的一部分.
①求圆的半径;
②要使高为3米的船通过,则其宽度须不超过多少米?

【答案】(1)①![]() ;②10;(2)①14.5;②
;②10;(2)①14.5;②![]() .
.
【解析】试题分析:(1)①利用待定系数法求函数解析式即可;②根据题意得出y=3时,求出x的值即可;
(2)①构造直角三角形利用BW2=BC2+CW2,求出即可;
②在RT△WGF中,由题可知,WF=14.5,WG=14.5﹣1=13.5,根据勾股定理知:GF2=WF2﹣WG2,求出即可.
试题解析:(1)①设抛物线解析式为: ![]() ,∵桥下水面宽度AB是20米,高CD是4米,∴A(﹣10,0),B(10,0),D(0,4),∴
,∵桥下水面宽度AB是20米,高CD是4米,∴A(﹣10,0),B(10,0),D(0,4),∴![]() ,解得:
,解得:  ,∴抛物线解析式为:
,∴抛物线解析式为: ![]() ;
;
②∵要使高为3米的船通过,∴![]() ,则
,则![]() ,解得:
,解得: ![]() ,∴EF=10米;
,∴EF=10米;
(2)①设圆半径r米,圆心为W,∵BW2=BC2+CW2,∴![]() ,解得:
,解得: ![]() ;
;
②在RT△WGF中,由题可知,WF=14.5,WG=14.5﹣1=13.5,根据勾股定理知:GF2=WF2﹣WG2,即GF2=14.52﹣13.52=28,所以GF=![]() ,此时宽度EF=
,此时宽度EF=![]() 米.
米.



 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
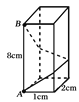
【题目】如图,长方体底面是长为2cm 宽为1cm的长方形,其高为8cm.
(1)如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,请利用侧面展开图计算所用细线最短需要多少?
(2)如果从点A开始经过4个侧面缠绕2圈到达点B,那么所用细线最短需要多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是一次函数![]() (x≥0)图象上一点,过点A作x轴的垂线l,B是l上一点(B在A上方),在AB的右侧以AB为斜边作等腰直角三角形ABC,反比例函数
(x≥0)图象上一点,过点A作x轴的垂线l,B是l上一点(B在A上方),在AB的右侧以AB为斜边作等腰直角三角形ABC,反比例函数![]() (x>0)的图象过点B,C,若△OAB的面积为6,则△ABC的面积是______.
(x>0)的图象过点B,C,若△OAB的面积为6,则△ABC的面积是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在第一象限内作射线OC,与x轴的夹角为60°,在射线OC上取一点A,过点A作AH⊥x 轴于点H,在抛物线y=x2(x>0)上取一点P,在y轴上取一点Q,使得以P、O、Q为顶点的三角形与△AOH全等,则符合条件的点A的坐标是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)与每件销售价x(元)的关系数据如下:
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元利润,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,△AOB、△COD是等腰直角三角形,点D在AB上.

(1)求证:△AOC≌△BOD;
(2)若AD=3,BD=1,求CD和△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某日孙老师佩戴运动手环进行快走锻炼,两次锻炼后数据如下表.与第一次锻炼相比,孙老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍.根据经验已知孙老师第二次锻炼时平均步长减少的百分率小于0.5.
项目 | 第一次锻炼 | 第二次锻炼 | ||
步数(步) | 10000 | ① | ||
平均步长(米/步) | 0.6 | ② | ||
距离(米) | 6000 | 7020 |
注:步数×平均步长=距离.
(1)求孙老师第二次锻炼时平均步长减少的百分率;
(2)孙老师发现好友中步数排名第一为24000步,因此在两次锻炼结束后又走了500米,使得总步数恰好为24000步,求孙老师这500米的平均步长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com