
【题目】函数![]() 是关于
是关于![]() 的二次函数,求:
的二次函数,求:
![]() 满足条件的
满足条件的![]() 值;
值;
![]() 为何值时,抛物线有最低点?求出这个最低点.这时,当
为何值时,抛物线有最低点?求出这个最低点.这时,当![]() 为何值时,
为何值时,![]() 随
随![]() 的增大而增大?
的增大而增大?
![]() 为何值时,函数有最大值?最大值是多少?这时,当
为何值时,函数有最大值?最大值是多少?这时,当![]() 为何值时,
为何值时,![]() 随
随![]() 的增大而减小.
的增大而减小.
【答案】![]() 满足条件的
满足条件的![]() 值为
值为![]() 或
或![]() ;
;![]() 抛物线的最低点为
抛物线的最低点为![]() ,当
,当![]() 时,
时,![]() 随
随![]() 的增大而增大;
的增大而增大;![]() 二次函数的最大值是
二次函数的最大值是![]() ,这时,当
,这时,当![]() 时,
时,![]() 随
随![]() 的增大而减小.
的增大而减小.
【解析】
(1)根据二次函数的定义得到m+2≠0且m2+m4=2,然后解两个不等式即可得到满足条件的m的值为2或3;
(2)根据二次函数的性质得当m+2>0时,抛物线有最低点,所以m=2,则y=4x2,然后根据二次函数的性质确定顶点坐标和增减性;
(3)根据二次函数的性质得到当m=3时,抛物线开口向下,函数有最大值,则y=x2,然后根据二次函数的性质确定最大值和增减性.
![]() 根据题意得
根据题意得![]() 且
且![]() ,
,
解得![]() ,
,![]() ,
,
所以满足条件的![]() 值为
值为![]() 或
或![]() ;
;
![]() 当
当![]() 时,抛物线有最低点,
时,抛物线有最低点,
所以![]() ,
,
抛物线解式为![]() ,
,
所以抛物线的最低点为![]() ,当
,当![]() 时,
时,![]() 随
随![]() 的增大而增大;
的增大而增大;
![]() 当
当![]() 时,抛物线开口向下,函数有最大值;
时,抛物线开口向下,函数有最大值;
抛物线解析式为![]() ,
,
所以二次函数的最大值是![]() ,这时,当
,这时,当![]() 时,
时,![]() 随
随![]() 的增大而减小.
的增大而减小.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】如图,连接在一起的两个等边三角形的边长都为1cm,一个微型机器人由点A开始按A→B→C→D→E→C→A→B→C…的顺序沿等边三角形的边循环移动.当微型机器人移动了2019cm后,它停在了点_____上.
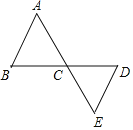
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形纸片分别沿两条不同的直线剪两刀,可以使剪得的三块纸片恰能拼成一个等腰三角形(不能有重叠和缝隙).小华的做法是:如图1所示,在矩形ABCD中,分别取AD、AB、CD的中点P、E、F,并沿直线PE 、PF剪两刀,所得的三部分可拼成等腰三角形△PMN (如图2).

(1)在图3中画出另一种剪拼成等腰三角形的示意图;
(2)以矩形ABCD的顶点B为原点,BC所在直线为x轴建立平面直角坐标系(如图4),矩形ABCD剪拼后得到等腰三角形△PMN,点P在边AD上(不与点A、D重合),点M、N在x轴上(点M在N的左边).如果点D的坐标为(5,8),直线PM的解析式为y=kx+b,求所有满足条件的k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BE、CE分别是∠ABC和∠ACB的平分线,过点E作DF∥BC交AB于D,交AC于F,若AB =5,AC =4,则△ADF周长为( ).

A.7B.8C.9D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为6,面积是36,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为______.
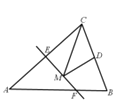
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,已知点A(-1,4),B(-2,2),C(1,1).

(1)作ΔABC关于x轴对称的△A1B1C1,并写出点A1,B1,C1的坐标,
(2)作△ABC关于y轴对称的△A2B2C2,并写出点A2,B2,C2的坐标,
(3)观察点A1,B1,C1和A2,B2,C2的坐标,请用文字语言归纳点A1和A2,B1和B2,C1和C2坐标之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
问题:如图,在正方形![]() 和平行四边形
和平行四边形![]() 中,点
中,点![]() ,
,![]() ,
,![]() 在同一条直线上,
在同一条直线上,![]() 是线段
是线段![]() 的中点,连接
的中点,连接![]() ,
,![]() .
.
探究:当![]() 与
与![]() 的夹角为多少度时,平行四边形
的夹角为多少度时,平行四边形![]() 是正方形?
是正方形?
小聪同学的思路是:首先可以说明四边形![]() 是矩形;然后延长
是矩形;然后延长![]() 交
交![]() 于点
于点![]() ,构造全等三角形,经过推理可以探索出问题的答案.
,构造全等三角形,经过推理可以探索出问题的答案.
请你参考小聪同学的思路,探究并解决这个问题.
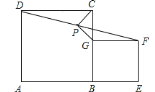
(1)求证:四边形![]() 是矩形;
是矩形;
(2)![]() 与
与![]() 的夹角为________度时,四边形
的夹角为________度时,四边形![]() 是正方形.
是正方形.
理由:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com