
【题目】已知,△ABC(如图).
(1)利用尺规按下列要求作图(保留作图痕迹,不写作法):
①作∠BAC的平分线AD,交BC于点D;
②作AB边的垂直平分线EF,分别交AD,AB于点E,F.
(2)连接BE,若∠ABC=60°,∠C=40°,求∠AEB的度数.

科目:初中数学 来源: 题型:
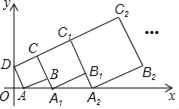
【题目】在平面直角坐标系中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2017个正方形的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:解一元二次不等式![]() .
.
解∵![]() ,∴
,∴![]() 可化为
可化为![]() .
.
由有理数的乘法法则:两数相乘,同号得正,得:①![]() ②
②![]()
解不等式组①,得![]() ,解不等式组②,得
,解不等式组②,得![]()
∴![]() 的解集为
的解集为![]() 或
或![]() .
.
即一元二次不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
(1)一元二次不等式![]() 的解集为____________;
的解集为____________;
(2)试解一元二次不等式![]() ;
;
(3)试解不等式![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线C:y=x2经过变化可得到抛物线C1:y1=a1x(x﹣b1),C1与x轴的正半轴交与点A1,且其对称轴分别交抛物线C,C1于点B1,D1,此时四边形OB1A1D1恰为正方形;按上述类似方法,如图2,抛物线C1:y1=a1x(x﹣b1)经过变换可得到抛物线C2:y2=a2x(x﹣b2),C2与x轴的正半轴交与点A2,且其对称轴分别交抛物线C1,C2于点B2,D2,此时四边形OB2A2D2也恰为正方形;按上述类似方法,如图3,可得到抛物线C3:y3=a3x(x﹣b3)与正方形OB3A3D3.请探究以下问题:
(1)填空:a1= ,b1= ;
(2)求出C2与C3的解析式;
(3)按上述类似方法,可得到抛物线Cn:yn=anx(x﹣bn)与正方形OBnAnDn(n≥1).
①请用含n的代数式直接表示出Cn的解析式;
②当x取任意不为0的实数时,试比较y2015与y2016的函数值的大小并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在数学课中学习了《解直角三角形》的内容后,双休日组织教学兴趣小组的小伙伴进行实地测量.如图,他们在坡度是i=1:2.5的斜坡DE的D处,测得楼顶的移动通讯基站铁塔的顶部A和楼顶B的仰角分别是60°、45°,斜坡高EF=2米,CE=13米,CH=2米.大家根据所学知识很快计算出了铁塔高AM.亲爱的同学们,相信你也能计算出铁塔AM的高度!请你写出解答过程.(数据 ![]() ≈1.41,
≈1.41, ![]() ≈1.73供选用,结果保留整数)
≈1.73供选用,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由正比例函数![]() 沿
沿![]() 轴的正方向平移4个单位而成的一次函数
轴的正方向平移4个单位而成的一次函数![]()
的图像与反比例函数![]() (
(![]() )在第一象限的图像交于A(1,n)和B两点.
)在第一象限的图像交于A(1,n)和B两点.
(1)求一次函数![]() 和反比例函数的解析式;
和反比例函数的解析式;
(2)求△ABO的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线相交于点O,分别过点C、D作CE∥BD、DE∥AC,CE、DE交于点E.

(1)求证:四边形OCED是菱形.
(2)将矩形ABCD改为菱形ABCD,其余条件不变,连结OE.若AC=10,BD=24,则OE的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果第一次租用2辆A型车和1辆B型车装运水果,一次运货10吨;第二次租用1辆A型车和2辆B型车装水果,一次运货11吨(两次运货都是满载)
①求每辆A型车和B型车满载时各装水果多少吨?
②现有31吨水果需运出,计划同时租用A型车和B型车一次运完,且每辆车都恰好装满,请设计出有哪几种租车方案?
③若A型车每辆租金200元,B型车每辆租金300元,问哪种租车方案最省钱,最省钱的方案总共租金多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com