
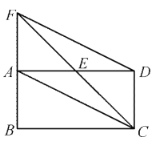
����Ŀ��С������ѧ����ѧϰ�ˡ���ֱ�������Ρ������ݺ�˫������֯��ѧ��ȤС���С������ʵ�ز�������ͼ���������¶���i=1��2.5��б��DE��D�������¥�����ƶ�ͨѶ��վ�����Ķ���A��¥��B�����Ƿֱ���60�㡢45����б�¸�EF=2�ף�CE=13�ף�CH=2�ף���Ҹ�����ѧ֪ʶ�ܿ�������������AM���װ���ͬѧ�ǣ�������Ҳ�ܼ��������AM�ĸ߶ȣ�����д�������̣������� ![]() ��1.41��
��1.41�� ![]() ��1.73��ѡ�ã��������������
��1.73��ѡ�ã��������������

���𰸡�17
�����������������
���¶�![]() ���EF=2�ɵ�FD=5�����CE=13��CH=2�ɵ�GD=18��DN=20���Ӷ���Rt��DBG�пɵ�BG=18����Rt��AND�пɽ��AN=
���EF=2�ɵ�FD=5�����CE=13��CH=2�ɵ�GD=18��DN=20���Ӷ���Rt��DBG�пɵ�BG=18����Rt��AND�пɽ��AN=![]() �������AM=AN-MN=AM-BG�������AM�ij�.
�������AM=AN-MN=AM-BG�������AM�ij�.
���������
��б�µ��¶���![]() ��EF=2��
��EF=2��
��FD=2.5EF=2.5��2=5��
��CE=13��CE=GF��
��GD=GF+FD=CE+FD=13+5=18��
��Rt��DBG������GDB=45�㣬
��BG=GD=18��
��Rt��DAN������NDA=60�㣬
��ND=NG+GD=CH+GD=2+18=20��
AN=NDtan60��=20��![]() =20
=20![]() ��
��
��AM=AN��MN=AN��BG=![]()
![]() ���ף���
���ף���
��������AMԼ17�ף�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������µ����ߣ��յ���������������ij�ҵ糬�ж�ÿ̨���۷ֱ�Ϊ![]() Ԫ��
Ԫ��![]() Ԫ��
Ԫ��![]() ��
��![]() �����ͺŵĿյ��������ܵ��������ͳ�����£�
�����ͺŵĿյ��������ܵ��������ͳ�����£�

��1����![]() ��
��![]() �����ͺſյ����ۼۣ�
�����ͺſյ����ۼۣ�
��2�����üҵ糬�����벻����![]() Ԫ���ʽ𣬲ɹ��������ͺŵĿյ�
Ԫ���ʽ𣬲ɹ��������ͺŵĿյ�![]() ̨����
̨����![]() ���ͺŵĿյ�����ܲɹ�����̨��
���ͺŵĿյ�����ܲɹ�����̨��
��3���ڣ�2���������£��üҵ糬��������![]() ̨�յ��ܷ�ɽʵ��������
̨�յ��ܷ�ɽʵ��������![]() Ԫ��Ŀ�ꣿ���ܣ�������ɹ�����.�����ܣ���˵������.
Ԫ��Ŀ�ꣿ���ܣ�������ɹ�����.�����ܣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �У���
����![]() ��
��![]() ���е㣬�ӳ�
���е㣬�ӳ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() ��
��![]() ��
��
��1����֤���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
��2����![]() ƽ��
ƽ��![]() ʱ��д��
ʱ��д��![]() ��
��![]() ��������ϵ����˵�����ɣ�
��������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �Ķ���OԲ�ģ��ʵ���Ϊ�뾶��������OA�ڵ�C����OB�ڵ�D���ٷֱ��Ե�C��DΪԲ�ģ�����
�Ķ���OԲ�ģ��ʵ���Ϊ�뾶��������OA�ڵ�C����OB�ڵ�D���ٷֱ��Ե�C��DΪԲ�ģ�����![]() �ij�Ϊ�뾶������������
�ij�Ϊ�뾶������������![]() �ڲ����ڵ�E��������OE������CD��������˵���������( )
�ڲ����ڵ�E��������OE������CD��������˵���������( )
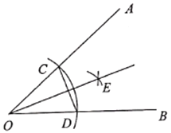
A. ����OE��![]() ��ƽ����B.
��ƽ����B. ![]() �ǵ���������
�ǵ���������
C. ֱ��OE��ֱƽ���߶�CDD. O��E�������CD����ֱ�߶Գ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Ϊ�˲���ij������BC�ĸ߶ȣ�С�����ڵ������ò������A����ý����ﶥ����������30�㣬Ȼ����ˮƽ�ض���������ǰ����50m����D������ʱ����һб�£��¶�i=1�� ![]() ������б��ǰ��20����E����ý����ﶥ����������45�㣬���¶�i=1��
������б��ǰ��20����E����ý����ﶥ����������45�㣬���¶�i=1�� ![]() ��ָ�����Ǧֱ�߶�FE��ˮƽ����DE�ıȣ������������ý�����BC�ĸ߶ȣ���ȡ
��ָ�����Ǧֱ�߶�FE��ˮƽ����DE�ıȣ������������ý�����BC�ĸ߶ȣ���ȡ![]() =1.732�������ȷ��0.1m����
=1.732�������ȷ��0.1m����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABC����ͼ����
��1�����ó߹水����Ҫ����ͼ��������ͼ�ۼ�����д��������
������BAC��ƽ����AD����BC�ڵ�D��
����AB�ߵĴ�ֱƽ����EF���ֱ�AD��AB�ڵ�E��F��
��2������BE������ABC��60������C��40�������AEB�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABC����ͼ����
��1�����ó߹水����Ҫ����ͼ��������ͼ�ۼ�����д��������
������BAC��ƽ����AD����BC�ڵ�D��
����AB�ߵĴ�ֱƽ����EF���ֱ�AD��AB�ڵ�E��F��
��2������BE������ABC��60������C��40�������AEB�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABCD�У��Խ���AC��BD�ཻ��O��EF����O����AF��BC��
��1����֤����BFO�ա�DEO��
��2����EFƽ����AEC�����ж��ı���AFCE����״����֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ��֯�����Ȱ��ܷ��������ܷ�����֪ʶ����������������ѧ���ijɼ����ܷ�100�֣���������50�֣�Ϊ�˽Ȿ�ξ����ijɼ��ֲ�����������ȡ������ѧ���ijɼ���Ϊ���������������������˲�������ͳ��ͼ�����������ͳ��ͼ������������⣮
ѧУ������ѧ���ɼ��ֲ�ͳ�Ʊ�
�����Σ��ɼ�Ϊx�֣� | Ƶ�� | Ƶ�� |
50��x��60 | 16 | 0.08 |
��60��x��70 | a | 0.31 |
��70��x��80 | 72 | 0.36 |
��80��x��90 | c | d |
��90��x��100 | 12 | b |
��1���˴γ�������������������� ����
��2��д�����е�a���� ����b���� ����c���� ����
��3����ȫѧ���ɼ��ֲ�ֱ��ͼ��
��4���������շ����ɸߵ�������һ���������Ƚ�������25%�IJ���ѧ���ܻ��һ�Ƚ�����һ�Ƚ��ķ������Ƕ��٣�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com