
【题目】随着气温的升高,空调的需求量大增,某家电超市对每台进价分别为![]() 元、
元、![]() 元的
元的![]() 、
、![]() 两种型号的空调,近两周的销售情况统计如下:
两种型号的空调,近两周的销售情况统计如下:

(1)求![]() 、
、![]() 两种型号空调的售价;
两种型号空调的售价;
(2)若该家电超市准备与不多于![]() 元的资金,采购这两种型号的空调
元的资金,采购这两种型号的空调![]() 台,求
台,求![]() 种型号的空调最多能采购多少台?
种型号的空调最多能采购多少台?
(3)在(2)的条件下,该家电超市售完这![]() 台空调能否山实现利润不低于
台空调能否山实现利润不低于![]() 元的目标?若能,请给出采购方案.若不能,请说明理由.
元的目标?若能,请给出采购方案.若不能,请说明理由.
【答案】(1)![]() 、
、![]() 两种型号空调的销售介分别为
两种型号空调的销售介分别为![]() 元和
元和![]() 元;(2)最多采购
元;(2)最多采购![]() 种型号的空调
种型号的空调![]() 台;(3)
台;(3)![]() 、
、![]() 两种型号的空调分别采购:
两种型号的空调分别采购:![]() 台和2
台和2![]() 台;
台;![]() 台和
台和![]() 台;
台;![]() 台和
台和![]() 台时,都可实现利润不低于
台时,都可实现利润不低于![]() 元的目标.
元的目标.
【解析】
(1)设A、B两种型号的空调的销售单价分别为x元、y元,根据6台A型号7台B型号的空调收入31000元,8台A型号11台B型号的空调收入45000元,列方程组求解;
(2)设采购A种型号的空调a台,则采购B种型号的空调(30-a)台,根据金额不多余54000元,列不等式求解;
(3)设利润为15800元,列不等式求出a的值,符合(2)的条件,可知能实现目标.
解:(1)设![]() 、
、![]() 两种型号的空调的销售价分别为
两种型号的空调的销售价分别为![]() 、
、![]() 元,
元,
则: ![]()
解得: ![]()
答:![]() 、
、![]() 两种型号空调的销售介分别为
两种型号空调的销售介分别为![]() 元和
元和![]() 元.
元.
(2)设采购![]() 种型号空调
种型号空调![]() 台,则采购
台,则采购![]() 种型号的空调
种型号的空调![]() 台
台
则![]() ,
,
解得:![]() ,
,
答:最多采购![]() 种型号的空调
种型号的空调![]() 台.
台.
(3)根据题意得:
![]() ,
,
解得![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴当![]() ,
,![]() ,
,
当![]() ,
,![]() ,
,
当![]() ,
,![]() ,
,
即:![]() 、
、![]() 两种型号的空调分别采购:
两种型号的空调分别采购:![]() 台和2
台和2![]() 台;
台;![]() 台和
台和![]() 台;
台;![]() 台和
台和![]() 台时,都可实现利润不低于
台时,都可实现利润不低于![]() 元的目标.
元的目标.
故答案为:(1)![]() 、
、![]() 两种型号空调的销售介分别为
两种型号空调的销售介分别为![]() 元和
元和![]() 元;(2)最多采购
元;(2)最多采购![]() 种型号的空调
种型号的空调![]() 台;(3)
台;(3)![]() 、
、![]() 两种型号的空调分别采购:
两种型号的空调分别采购:![]() 台和2
台和2![]() 台;
台;![]() 台和
台和![]() 台;
台;![]() 台和
台和![]() 台时,都可实现利润不低于
台时,都可实现利润不低于![]() 元的目标.
元的目标.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②3b+2c<0;③4a+c<2b;④m(am+b)+b<a(m≠1),其中结论正确的个数是( )

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30°,点P是∠AOB内的定点,且OP=3.若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是( )

A.12B.9C.6D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像相交于
的图像相交于![]() 、
、![]() 两点.
两点.

(1)求出两函数解析式;
(2)根据图像回答:当![]() 为何值时,一次函数的函数值大于反比例函数的函数值?
为何值时,一次函数的函数值大于反比例函数的函数值?
(3)连接![]() 、
、![]() ,试求
,试求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地为了解青少年实力情况,现随机抽查了若干名初中学生进行视力情况统计,分为视力正常、轻度近视、重度近视三种情况,并绘成如图所示的条形统计图和扇形统计图(不完整),请你根据图中信息解答下列问题:

(1)求这次被抽查的学生一共有多少人?
(2)求被抽查的学生中轻度近视的学生人数,并将条形统计图补充完整;
(3)若某地有![]() 万名初中生,请估计视力不正常(包括轻度近视、重度近视)的学生共有多少人?
万名初中生,请估计视力不正常(包括轻度近视、重度近视)的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
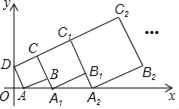
【题目】在平面直角坐标系中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2017个正方形的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1:![]() ,求旗杆AB的高度(
,求旗杆AB的高度(![]() ≈1.7,结果精确到个位).
≈1.7,结果精确到个位).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在数学课中学习了《解直角三角形》的内容后,双休日组织教学兴趣小组的小伙伴进行实地测量.如图,他们在坡度是i=1:2.5的斜坡DE的D处,测得楼顶的移动通讯基站铁塔的顶部A和楼顶B的仰角分别是60°、45°,斜坡高EF=2米,CE=13米,CH=2米.大家根据所学知识很快计算出了铁塔高AM.亲爱的同学们,相信你也能计算出铁塔AM的高度!请你写出解答过程.(数据 ![]() ≈1.41,
≈1.41, ![]() ≈1.73供选用,结果保留整数)
≈1.73供选用,结果保留整数)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com