
【题目】如图,以![]() 的顶点O圆心,适当长为半径画弧,交OA于点C,交OB于点D.再分别以点C、D为圆心,大于
的顶点O圆心,适当长为半径画弧,交OA于点C,交OB于点D.再分别以点C、D为圆心,大于![]() 的长为半径画弧,两弧在
的长为半径画弧,两弧在![]() 内部交于点E.作射线OE,连接CD.则下列说法错误的是( )
内部交于点E.作射线OE,连接CD.则下列说法错误的是( )
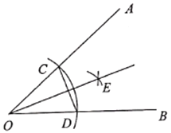
A. 射线OE是![]() 的平分线B.
的平分线B. ![]() 是等腰三角形
是等腰三角形
C. 直线OE垂直平分线段CDD. O、E两点关于CD所在直线对称
【答案】D
【解析】
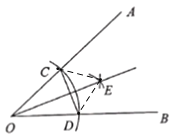
连接CE、DE,根据作图得到OC=OD、CE=DE,利用SSS证得△EOC≌△EOD从而证明得到射线OE平分∠AOB,判断A正确;根据作图得到OC=OD,判断B正确;根据作图得到OC=OD,由A得到射线OE平分∠AOB,根据等腰三角形三线合一的性质得到OE是CD的垂直平分线,判断C正确;根据作图不能得出CD平分OE,判断D错误.
A、连接CE、DE,根据作图得到OC=OD、CE=DE,
又OE是公共边,
∴△EOC≌△EOD(SSS),
∴∠AOE=∠BOE,即射线OE是∠AOB的平分线,故A选项正确,不符合题意;
B、根据作图得到OC=OD,
∴△COD是等腰三角形,故B选项正确,不符合题意;
C、根据作图得到OC=OD,
又∵射线OE平分∠AOB,
∴OE是CD的垂直平分线,故C选项正确,不符合题意;
D、根据作图不能得出CD平分OE,
∴CD不是OE的平分线,
∴O、E两点关于CD所在直线不对称,故D选项错误,符合题意,
故选D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像相交于
的图像相交于![]() 、
、![]() 两点.
两点.

(1)求出两函数解析式;
(2)根据图像回答:当![]() 为何值时,一次函数的函数值大于反比例函数的函数值?
为何值时,一次函数的函数值大于反比例函数的函数值?
(3)连接![]() 、
、![]() ,试求
,试求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:解一元二次不等式![]() .
.
解∵![]() ,∴
,∴![]() 可化为
可化为![]() .
.
由有理数的乘法法则:两数相乘,同号得正,得:①![]() ②
②![]()
解不等式组①,得![]() ,解不等式组②,得
,解不等式组②,得![]()
∴![]() 的解集为
的解集为![]() 或
或![]() .
.
即一元二次不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
(1)一元二次不等式![]() 的解集为____________;
的解集为____________;
(2)试解一元二次不等式![]() ;
;
(3)试解不等式![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
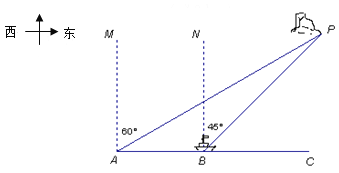
【题目】海中有一个小岛P,它的周围18海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A测得小岛P在北偏东60°方向上,航行12海里到达B点,这时测得小岛P在北偏东45°方向上.如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线C:y=x2经过变化可得到抛物线C1:y1=a1x(x﹣b1),C1与x轴的正半轴交与点A1,且其对称轴分别交抛物线C,C1于点B1,D1,此时四边形OB1A1D1恰为正方形;按上述类似方法,如图2,抛物线C1:y1=a1x(x﹣b1)经过变换可得到抛物线C2:y2=a2x(x﹣b2),C2与x轴的正半轴交与点A2,且其对称轴分别交抛物线C1,C2于点B2,D2,此时四边形OB2A2D2也恰为正方形;按上述类似方法,如图3,可得到抛物线C3:y3=a3x(x﹣b3)与正方形OB3A3D3.请探究以下问题:
(1)填空:a1= ,b1= ;
(2)求出C2与C3的解析式;
(3)按上述类似方法,可得到抛物线Cn:yn=anx(x﹣bn)与正方形OBnAnDn(n≥1).
①请用含n的代数式直接表示出Cn的解析式;
②当x取任意不为0的实数时,试比较y2015与y2016的函数值的大小并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在数学课中学习了《解直角三角形》的内容后,双休日组织教学兴趣小组的小伙伴进行实地测量.如图,他们在坡度是i=1:2.5的斜坡DE的D处,测得楼顶的移动通讯基站铁塔的顶部A和楼顶B的仰角分别是60°、45°,斜坡高EF=2米,CE=13米,CH=2米.大家根据所学知识很快计算出了铁塔高AM.亲爱的同学们,相信你也能计算出铁塔AM的高度!请你写出解答过程.(数据 ![]() ≈1.41,
≈1.41, ![]() ≈1.73供选用,结果保留整数)
≈1.73供选用,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】开学前,小强、小亮和小伟去文化用品商店购买笔和本,小强用17元买了1支笔和4个本,小亮用19元买了2支笔和3个本,小伟购买上述价格的笔和本共用了48元,且本的数量不少于笔的数量,则小伟的购买方案共有( )
A. 1种B. 2种C. 3种D. 4种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com