
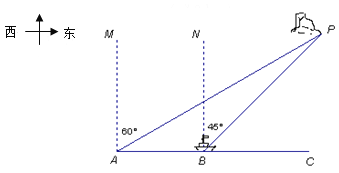
【题目】海中有一个小岛P,它的周围18海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A测得小岛P在北偏东60°方向上,航行12海里到达B点,这时测得小岛P在北偏东45°方向上.如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由.
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】在学习了轴对称知识之后,数学兴趣小组的同学们对课本习题进行了深入研究,请你跟随兴趣小组的同学,一起完成下列问题.
(1)(课本习题)如图①,△ABC是等边三角形,BD是中线,延长BC至E,使CE=CD. 求证:DB=DE
(2)(尝试变式)如图②,△ABC是等边三角形,D是AC边上任意一点,延长BC至E,使CE=AD.
求证:DB=DE.
(3)(拓展延伸)如图③,△ABC是等边三角形,D是AC延长线上任意一点,延长BC至E,使CE=AD请问DB与DE是否相等? 并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:我们把对角线相等的四边形叫做和美四边形.
![]() 请举出一种你所学过的特殊四边形中是和美四边形的例子.
请举出一种你所学过的特殊四边形中是和美四边形的例子.
![]() 如图1,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,已知四边形EFGH是菱形,求证:四边形ABCD是和美四边形;
如图1,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,已知四边形EFGH是菱形,求证:四边形ABCD是和美四边形;
![]() 如图2,四边形ABCD是和美四边形,对角线AC,BD相交于O,
如图2,四边形ABCD是和美四边形,对角线AC,BD相交于O,![]() ,E、F分别是AD、BC的中点,请探索EF与AC之间的数量关系,并证明你的结论.
,E、F分别是AD、BC的中点,请探索EF与AC之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以![]() 的顶点O圆心,适当长为半径画弧,交OA于点C,交OB于点D.再分别以点C、D为圆心,大于
的顶点O圆心,适当长为半径画弧,交OA于点C,交OB于点D.再分别以点C、D为圆心,大于![]() 的长为半径画弧,两弧在
的长为半径画弧,两弧在![]() 内部交于点E.作射线OE,连接CD.则下列说法错误的是( )
内部交于点E.作射线OE,连接CD.则下列说法错误的是( )
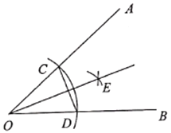
A. 射线OE是![]() 的平分线B.
的平分线B. ![]() 是等腰三角形
是等腰三角形
C. 直线OE垂直平分线段CDD. O、E两点关于CD所在直线对称
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量某建筑物BC的高度,小明先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地而上向建筑物前进了50m到达D处,此时遇到一斜坡,坡度i=1: ![]() ,沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°,(坡度i=1:
,沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°,(坡度i=1: ![]() 是指坡面的铅直高度FE与水平宽度DE的比).请你计算出该建筑物BC的高度.(取
是指坡面的铅直高度FE与水平宽度DE的比).请你计算出该建筑物BC的高度.(取![]() =1.732,结果精确到0.1m).
=1.732,结果精确到0.1m).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC(如图).
(1)利用尺规按下列要求作图(保留作图痕迹,不写作法):
①作∠BAC的平分线AD,交BC于点D;
②作AB边的垂直平分线EF,分别交AD,AB于点E,F.
(2)连接BE,若∠ABC=60°,∠C=40°,求∠AEB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)试判断AB与AF,EB之间存在的数量关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com