
【题目】如图,在![]() 中,
中,![]() 的垂直平分线交
的垂直平分线交![]() 边于点
边于点![]() 的垂 直平分线交
的垂 直平分线交![]() 边于点
边于点![]() .
.
![]() 求
求![]() 的周长.
的周长.
![]() 求
求![]() 的度数.
的度数.
![]() 判断△AEN 的形状并证明.
判断△AEN 的形状并证明.

【答案】(1)12;(2)60°;(3)△AEN为等边三角形,理由见详解.
【解析】
(1)根据题意,利用线段垂直平分线性质得到AE=BE,AN=CN,等量代换即可确定出三角形AEN周长;
(2)由等边对等角,以及三角形内角和定理求出所求角度数即可;
(3)根据题意利用外角性质确定出三角形AEN三个角都为60°,即可确定出三角形形状.
解:(1)∵AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点N,
∴AE=BE,AN=CN,
∵BC=12,
∴△AEN周长l=AE+EN+AN=BE+EN+NC=BC=12;
(2)∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵AE=BE,AN=CN,
∴∠BAE=∠CAN=30°,
∴∠EAN=∠BAC-∠BAE-∠CAN=60°;
(3)△AEN为等边三角形,理由如下:
∵∠AEN=∠B+∠BAE=60°,∠ANE=∠C+∠CAN=60°,
∴△AEN为等边三角形.


科目:初中数学 来源: 题型:
【题目】如图,![]() 是边长为4cm的正方形
是边长为4cm的正方形![]() 对角线的交点,
对角线的交点,![]() 是
是![]() 的中点,动点
的中点,动点![]() 由点
由点![]() 开始沿折线
开始沿折线![]() 方向匀速运动,到点
方向匀速运动,到点![]() 时停止运动,速度为
时停止运动,速度为![]() .设
.设![]() 点的运动时间为
点的运动时间为![]() ,点
,点![]() 的运动路径与
的运动路径与![]() 、
、![]() 所围成的图形面积为
所围成的图形面积为![]() ,则描述面积
,则描述面积![]() 与时间
与时间![]() 的关系的图象是( )
的关系的图象是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地为了解青少年实力情况,现随机抽查了若干名初中学生进行视力情况统计,分为视力正常、轻度近视、重度近视三种情况,并绘成如图所示的条形统计图和扇形统计图(不完整),请你根据图中信息解答下列问题:

(1)求这次被抽查的学生一共有多少人?
(2)求被抽查的学生中轻度近视的学生人数,并将条形统计图补充完整;
(3)若某地有![]() 万名初中生,请估计视力不正常(包括轻度近视、重度近视)的学生共有多少人?
万名初中生,请估计视力不正常(包括轻度近视、重度近视)的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1:![]() ,求旗杆AB的高度(
,求旗杆AB的高度(![]() ≈1.7,结果精确到个位).
≈1.7,结果精确到个位).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,一次函数y=kx+b(k≠0)的图象与反比例函数![]() (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n)。线段OA=5,E为x轴上一点,且
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n)。线段OA=5,E为x轴上一点,且![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)求△AOC的面积;
(3)直接写出一次函数值大于反比例函数自变量x的取值范围。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】海中有一个小岛P,它的周围18海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A测得小岛P在北偏东60°方向上,航行12海里到达B点,这时测得小岛P在北偏东45°方向上.如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由.
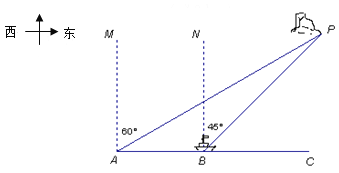
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】假设某商场地下停车场有5个出入口,每天早晨7点开始对外停车且此时车位空置率为80%,在每个出入口的车辆数均是匀速出入的情况下,如果开放2个进口和3个出口,8小时车库恰好停满;如果开放3个进口和2个出口,2小时车库恰好停满2019年元旦节期间,由于商场人数增多,早晨7点时的车位空置率变为60%,又因为车库改造,只能开放2个进口和1个出口,则从早晨7点开始经过_____小时车库恰好停满.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com