Question

【题目】解下列不等式（组），并把题的解集在数轴上表示出来；

Answer 1

【答案】（1）；（2）x＜-12；（3）-3＜x＜1，图见详解；（4）1≤x＜4，图见详解.

【解析】

（1）由题意先移项，再去分母，化系数为1即可；

（2）根据题意先去括号，再移项，合并同类项，把x的系数化为1即可；

（3）由题意分别求出各不等式的解集，再求出其公共解集，并在数轴上表示出来即可；

（4）根据题意分别求出各不等式的解集，再求出其公共解集，并在数轴上表示出来即可．

解：（1）

移项得：，

去分母得：，

把x的系数化为1得：.

（2）

去括号得：-6+2x＞3x+6，

移项得：2x-3x＞6+6，

合并同类项得：-x＞12，

把x的系数化为1得：x＜-12.

（3），

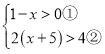由①得，x＜1，

由②得，x＞-3，

故不等式组的解集为：-3＜x＜1．

在数轴上表示为：

（4），

由①得，x≥1，由②得，x＜4，

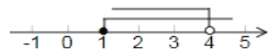
故不等式组的解集为：1≤x＜4．

在数轴上表示为：