
【题目】在学习了轴对称知识之后,数学兴趣小组的同学们对课本习题进行了深入研究,请你跟随兴趣小组的同学,一起完成下列问题.
(1)(课本习题)如图①,△ABC是等边三角形,BD是中线,延长BC至E,使CE=CD. 求证:DB=DE
(2)(尝试变式)如图②,△ABC是等边三角形,D是AC边上任意一点,延长BC至E,使CE=AD.
求证:DB=DE.
(3)(拓展延伸)如图③,△ABC是等边三角形,D是AC延长线上任意一点,延长BC至E,使CE=AD请问DB与DE是否相等? 并证明你的结论.

【答案】(1)见详解;(2)见详解;(3)DB=DE成立,证明见详解
【解析】
(1)由等边三角形的性质,得到∠CBD=30°,∠ACB=60°,由CD=CE,则∠E=∠CDE=30°,得到∠E=∠CBD=30°,即可得到DB=DE;
(2)过点D作DG∥AB,交BC于点G,证明△BDC≌△EDG,根据全等三角形的性质证明结论;
(3)过点D作DF∥AB交BE于F,由“SAS”可证△BCD≌△EFD,可得DB=DE.
证明:(1)∵△ABC是等边三角形
∴∠ABC=∠BCA=60°,
∵点D为线段AC的中点,
∴BD平分∠ABC,AD=CD,
∴∠CBD=30°,
∵CD=CE,
∴∠CDE=∠CED,
又∵∠CDE+∠CED=∠BCD,
∴2∠CED=60°,
∴∠CED=30°=∠CBD,
∴DB=DE;
(2)过点D作DG∥AB,交BC于点G,如图,
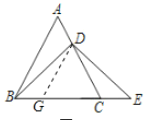
∴∠DGC=∠ABC=60°,又∠DCG=60°,
∴△DGC为等边三角形,
∴DG=GC=CD,
∴BC-GC=AC-CD,即AD=BG,
∵AD=CE,
∴BG=CE,
∴BC=GE,
在△BDC和△EDG中,
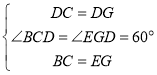 ,
,
∴△BDC≌△EDG(SAS)
∴BD=DE;
(3)DB=DE成立,
理由如下:过点D作DF∥AB交BE于F,

∴∠CDF=∠A,∠CFD=∠ABC,
∵△ABC是等边三角形
∴∠ABC=∠BCA=∠A=60°,BC=AC=AB,
∴∠CDF=∠CFD=60°=∠ACB=∠DCF,
∴△CDF为等边三角形
∴CD=DF=CF,
又AD=CE,
∴AD-CD=CE-CF,
∴BC=AC=EF,
∵∠BCD=∠CFD+∠CDF=120°,
∠DFE=∠FCD+∠FDC=120°,
∴∠BCD=∠DFE,且BC=EF,CD=DF,
∴△BCD≌△EFD(SAS)
∴DB=DE.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】小红和小明在操场做游戏,他们先在地上画了半径分别2m和3m的同心圆(如图),蒙上眼在一定距离外向圈内掷小石子,掷中阴影小红胜,否则小明胜,未掷入圈内不算,你来当裁判.
(1)你认为游戏公平吗?为什么?
(2)游戏结束,小明边走边想,“反过来,能否用频率估计概率的方法,来估算某一不规则图形的面积呢”.请你设计方案,解决这一问题.(要求补充完整图形,说明设计步骤、原理,写出估算公式)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是边长为4cm的正方形
是边长为4cm的正方形![]() 对角线的交点,
对角线的交点,![]() 是
是![]() 的中点,动点
的中点,动点![]() 由点
由点![]() 开始沿折线
开始沿折线![]() 方向匀速运动,到点
方向匀速运动,到点![]() 时停止运动,速度为
时停止运动,速度为![]() .设
.设![]() 点的运动时间为
点的运动时间为![]() ,点
,点![]() 的运动路径与
的运动路径与![]() 、
、![]() 所围成的图形面积为
所围成的图形面积为![]() ,则描述面积
,则描述面积![]() 与时间
与时间![]() 的关系的图象是( )
的关系的图象是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30°,点P是∠AOB内的定点,且OP=3.若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是( )

A.12B.9C.6D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,以△ABC的边AB为直径的⊙O交边BC于点E,过点E作⊙O的切线交AC于点D,且ED⊥AC.


(1)试判断△ABC的形状,并说明理由;
(2)如图2,若线段AB、DE的延长线交于点F,∠C=75°,CD=![]() ,求⊙O的半径和BF的长
,求⊙O的半径和BF的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像相交于
的图像相交于![]() 、
、![]() 两点.
两点.

(1)求出两函数解析式;
(2)根据图像回答:当![]() 为何值时,一次函数的函数值大于反比例函数的函数值?
为何值时,一次函数的函数值大于反比例函数的函数值?
(3)连接![]() 、
、![]() ,试求
,试求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地为了解青少年实力情况,现随机抽查了若干名初中学生进行视力情况统计,分为视力正常、轻度近视、重度近视三种情况,并绘成如图所示的条形统计图和扇形统计图(不完整),请你根据图中信息解答下列问题:

(1)求这次被抽查的学生一共有多少人?
(2)求被抽查的学生中轻度近视的学生人数,并将条形统计图补充完整;
(3)若某地有![]() 万名初中生,请估计视力不正常(包括轻度近视、重度近视)的学生共有多少人?
万名初中生,请估计视力不正常(包括轻度近视、重度近视)的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1:![]() ,求旗杆AB的高度(
,求旗杆AB的高度(![]() ≈1.7,结果精确到个位).
≈1.7,结果精确到个位).

查看答案和解析>>
科目:初中数学 来源: 题型:
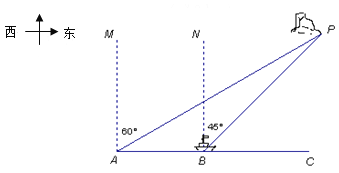
【题目】海中有一个小岛P,它的周围18海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A测得小岛P在北偏东60°方向上,航行12海里到达B点,这时测得小岛P在北偏东45°方向上.如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com