
【题目】在平面直角坐标系中,已知A(a,b),B(2,2),且|a-b+8|+![]() =0.
=0.
(1)求点A的坐标;
(2)过点A作AC⊥x轴于点C,连接BC,AB,延长AB交x轴于点D,设AB交y轴于点E,那么OD与OE是否相等?请说明理由.
(3)在x轴上是否存在点P,使S△OBP=S△BCD?若存在,请求出P点坐标,若不存在,请说明理由.
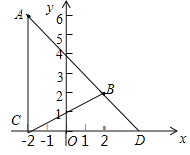
【答案】(1)点A的坐标为(-2,6);(2)OD与OE相等.理由见解析;(3)存在. P(-6,0)或(6,0).
【解析】
(1)利用非负数的性质解决问题即可.
(2)如图2,OD与OE相等.通过计算证明OE=4,OD=4即可解决问题.
(3)假设存在.设P(m,0),构建方程求出m即可解决问题.
(1)由|a-b+8|+![]() =0,
=0,
![]() ,
,
解得:![]() .
.
∴点A的坐标为(-2,6);
(2)如图2,OD与OE相等.理由如下:
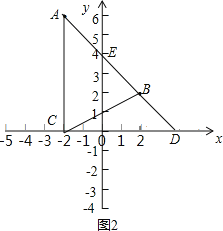
设点D的坐标为(x,0)(x>0),点E的坐标为(0,y)(y>0),
则CD=x+2,OE=y,
因为,三角形ABC的面积=三角形ACD的面积-三角形BCD的面积,
所以,12=![]() ×(x+2)×6-
×(x+2)×6-![]() ×(x+2)×2=2(x+2),
×(x+2)×2=2(x+2),
解得,x=4,即OD=4.
又因为,三角形EOD的面积=三角形ACD的面积-梯形ACOE的面积,
所以,![]() ×4×y=
×4×y=![]() ×6×6-
×6×6-![]() ×(y+6)×2,
×(y+6)×2,
解得:y=4,即OE=4,
所以,OD=OE.
(3)存在.设P(m,0),
由题意:![]() |m|×2=6,
|m|×2=6,
解得m=±6,
∴P(-6,0)或(6,0).


科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O, ∠AOM=90°,

(1)如图1,若OC平分∠AOM.求∠AOD的度数;
(2)如图2,若∠BOC=4∠NOB,且OM平分∠NOC,求∠MON的度数;
查看答案和解析>>
科目:初中数学 来源: 题型:
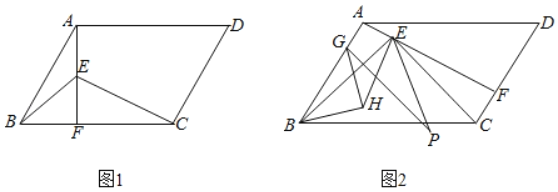
【题目】如图,ABCD中,E为平行四边形内部一点,连接AE,BE,CE.
(1)如图1,AE⊥BC交BC于点F,已知∠EBC=45°,∠BAF=∠ECF,AB=![]() ,EF=1,求AD的长;
,EF=1,求AD的长;
(2)如图2,AE⊥CD交CD于点F,AE=CF且∠BEC=90°,G为AB上一点,作GP⊥BE且GP=CE,并以BG为斜边作等腰Rt△BGH,连接EP、EH.求证:EP=![]() EH.
EH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E.
(1)若∠DBC=25°,求∠ADC′的度数;
(2)若AB=4,AD=8,求△BDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC 中,∠BAC=90°,AB=AC=2,以 AC 为一边.在△ABC 外部作等腰直角三角形ACD ,则线段 BD 的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点,且EG、FH交于点O.若AC=4,则EG2+FH2=______.
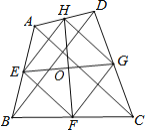
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在班上组织的一次晚会中,小丽和小芳都想当节目主持人,但现在只有一个名额.小芳想出了一个用游戏来选人的办法,她将一个转盘平均分成6份,如图所示.游戏规定:随意转动转盘,若指针指到偶数,则小丽去;若指针指到奇数,则小芳去.
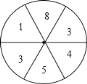
(1)指针指到偶数的概率是多少?指针指到奇数的概率是多少?
(2)这个游戏对双方公平吗?为什么?若游戏不公平,请你修改转盘中的数字,使得游戏对双方公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
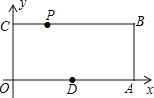
【题目】已知,如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,动点P在线段BC上以每秒2个单位长的速度由点C向B 运动.设 动点P的运动时间为t秒
(1)当t为何值时,四边形PODB是平行四边形?
(2)在直线CB上是否存在一点Q,使得O、D、Q、P四点为顶点的四边形是菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由。
(3) 在线段PB上有一点M,且PM=5,当P运动 秒时,四边形OAMP的周长最小, 并画图标出点M的位置。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在方格纸中
(1)请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),并求出B点坐标;
(2)以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形△A′B′C′;
(3)计算△A′B′C′的面积S.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com