
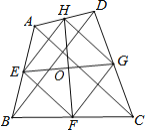
【题目】如图,在四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点,且EG、FH交于点O.若AC=4,则EG2+FH2=______.
【答案】16
【解析】
根据三角形的中位线定理和菱形的判定,可得顺次连接对角线相等的四边形各边中点所得四边形是菱形;根据菱形的性质得到EG⊥HF,且EG=2OE,FH=2OH.在Rt△OEH中,根据勾股定理得到OE2+OH2=EH2=4,再根据等式的性质,在等式的两边同时乘以4,根据4=22,把等式进行变形,并把EG=2OE,FH=2OH代入变形后的等式中,即可求出EG2+FH2的值.
∵E、F、G、H分别是线段AB、BC、CD、AD的中点,
∴EH、FG分别是△ABD、△BCD的中位线,
EF、HG分别是△ABC、△ACD的中位线,
根据三角形的中位线的性质知,EH=FG![]() BD,EF=HG
BD,EF=HG![]() AC.
AC.
又∵AC=BD,
∴EH=FG=EF=HG,
∴四边形EFGH是菱形,
∴EG⊥FH,EG=2OE,FH=2OH.
在Rt△OEH中,根据勾股定理得:OE2+OH2=EH2=4,
等式两边同时乘以4得:4OE2+4OH2=4×4=16,
∴(2OE)2+(2OH)2=16,
即EG2+FH2=16.
故答案为:16.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=8,CF=6,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在某一次实验中,测得两个变量之间的关系如下表所示:
自变量x | 1 | 2 | 3 | 4 | 12 | |
因变量y | 12.03 | 5.98 | 3.04 | 1.99 | 1.00 |
请你根据表格回答下列问题:
① 这两个变量之间可能是怎样的函数关系?你是怎样作出判断的?请你简要说明理由。
②请你写出这个函数的解析式。
③表格中空缺的数值可能是多少?请你给出合理的数值。
查看答案和解析>>
科目:初中数学 来源: 题型:
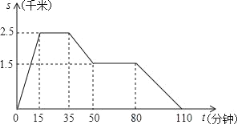
【题目】一天,王亮同学从家里跑步到体育馆,在那里锻炼了一阵后又走到某书店去买书,然后散步走回家如图反映的是在这一过程中,王亮同学离家的距离s(千米)与离家的时间t(分钟)之间的关系,请根据图象解答下列问题:
(1)体育馆离家的距离为多少千米,书店离家的距离为多少千米;王亮同学在书店待了多少分钟.
(2)分别求王亮同学从体育馆走到书店的平均速度和从书店出来散步回家的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
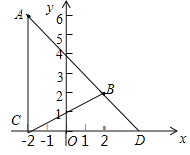
【题目】在平面直角坐标系中,已知A(a,b),B(2,2),且|a-b+8|+![]() =0.
=0.
(1)求点A的坐标;
(2)过点A作AC⊥x轴于点C,连接BC,AB,延长AB交x轴于点D,设AB交y轴于点E,那么OD与OE是否相等?请说明理由.
(3)在x轴上是否存在点P,使S△OBP=S△BCD?若存在,请求出P点坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达B处,又测得信号塔顶端C的仰角为45°,CE⊥AB于点E,E、B、A在一条直线上.则信号塔CD的高度为( )

A. 20![]() 米 B. (20
米 B. (20![]() -8)米 C. (20
-8)米 C. (20![]() -28)米 D. (20
-28)米 D. (20![]() -20)米
-20)米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温度的变化是人们在生活中经常谈论的话题,请你根据下图回答下列问题:
(1)上午9时的温度是多少?这一天的最高温度是多少?
(2)这一天的温差是多少?从最低温度到最高温度经过了多长时间?
(3)在什么时间范围内温度在下降?图中的A点表示的是什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,BC=8,将矩形ABCD沿CE折叠后,使点D恰好落在对角线AC上的点F处.
(1)求EF的长;
(2)求梯形ABCE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+8(k<0)交y轴于点A,交x轴于点B.将△AOB关于直线AB翻折得到△APB.过点A作AC∥x轴交线段BP于点C,在AC上取点D,且点D在点C的右侧,连结BD.
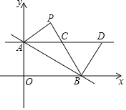
(1)求证:AC=BC
(2)若AC=10.
①求直线AB的表达式.
②若△BCD是以BC为腰的等腰三角形,求AD的长.
(3)若BD平分∠OBP的外角,记△APC面积为S1,△BCD面积为S2,且![]() =
=![]() ,则
,则![]() 的值为______(直接写出答案)
的值为______(直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com